【Java】快速排序

快速排序是由冒泡排序演变而来，比冒泡排序更快的排序算法。之所以快，是因为快速排序用了分治法。

相同的是，与冒泡排序一样，快速排序也属于交换排序，通过元素之间的比较和交换来排序。

不同的是，冒泡排序每一轮只把一个元素冒泡到数列的一端，而快速排序每轮挑选一个基准元素，让比它小的元素移动到一端，让比它大的元素移动到另一端，从而把数列拆解成两个部分。

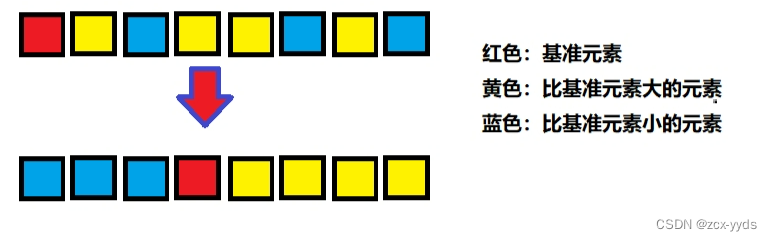
这种每次将数列分为两个部分的方法就叫做分治法。

分治法的好处体现在相比于冒泡排序它会有更小的时间复杂度，对于n的元素的冒泡排序时间复杂度为O(n²),而快速排序总体的平均时间复杂度为O(nlogn)。

在使用分治法的过程中以基准元素为中心把其他元素移到它的两边，那么如何选择基准元素呢？

1、选择第一个元素

最简单的方法是直接选择数列第一个元素为基准元素，但是这种方法在有些特殊情况下会出现问题：

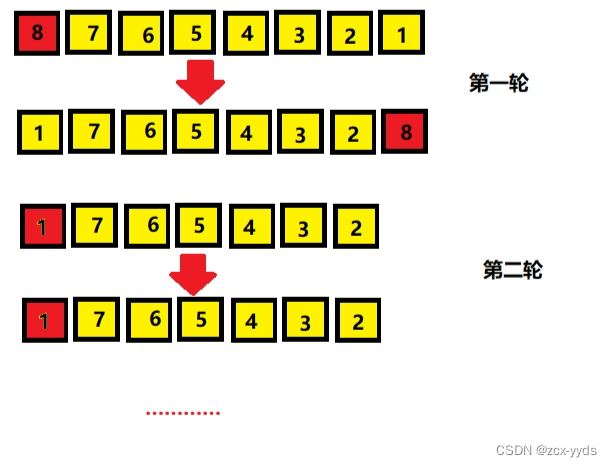
对于这种原本是逆序的数列，每轮都只能确定基准元素的位置，这种情况下快速排序需要进行n轮，时间复杂度退化到了O(n²)。

2、随机选择

为了解决时间复杂度过大的情况，我们可以随机选择一个元素，并与首位元素互换位置，虽然这种情况下也有几率选到数列的最大或最小值，但大多情况下都是可以的。

所以，虽然快速排序的平均时间复杂度为O(nlogn)，但最坏情况下也可以达到O(n²)。

选好了基准元素，就要将其他元素移到基准元素两边，具体实现有两种方法：

• 双边循环法
• 单边循环法

1、双边循环法

对以下数列按从小到大进行排序：

首先，选定基准元素p，并设置左右两个指针 l 和 r

开始循环后，从r指针开始，让r指针元素与基准元素做比较，如果大于等于p，则r指针向左移动；如果小于p，则停止移动，换到l指针。

对于当前数列，r指针元素为1，1<4，所以r指针停止移动，换到l指针。

换到l指针后，让l指针元素与基准元素做比较，如果小于等于p，则r指针向右移动；如果大于p，则停止移动。

按照此思路，后续步骤如下：

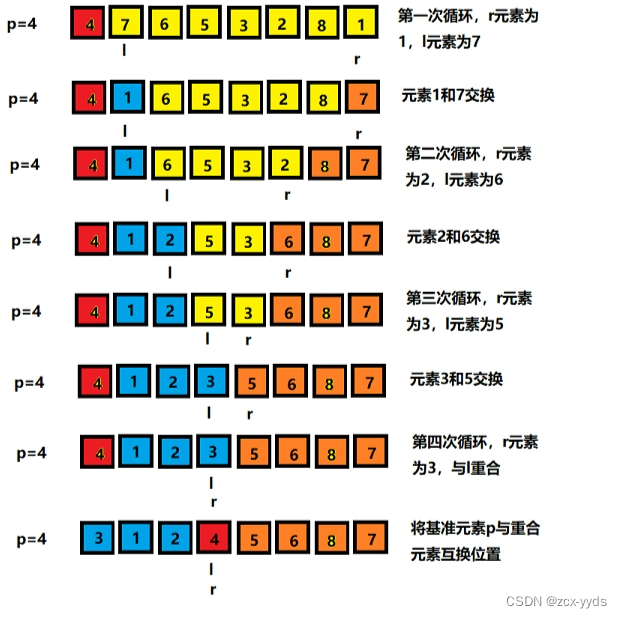
实现代码如下：

import java.util.Arrays;public class quickSort {    public static void quickSort(int arr[],int startIndex,int endIndex){        //递归结束条件为startIndex大于或等于endIndex        if(startIndex>=endIndex){            return;        }        //得到基准元素位置        int pIndex=partition(arr,startIndex,endIndex);        //根据基准元素分两部分进行递归排序        quickSort(arr,startIndex,pIndex-1);        quickSort(arr,pIndex+1,endIndex);    }        public static int partition(int arr[],int startIndex,int endIndex)    {        int p=arr[startIndex];//基准元素(可取随机位置)        int l=startIndex;//左指针        int r=endIndex;//右指针        while(l!=r){            //控制右指针向左移动，找到小于基准元素的那个数            while((lp)){                r--;            }            //控制左指针向右移动，找到大于基准元素的那个数            while((l                l++;            }            //交换l指针和r指针所指的元素            if(l                int tmp=arr[l];                arr[l]=arr[r];                arr[r]=tmp;            }        }        //交换基准元素和重合点的元素        arr[startIndex]=arr[l];        arr[l]=p;        return l;    }    public static void main(String[] args) {        int arr[]={4,7,6,5,3,2,8,1};        quickSort(arr,0,7);        System.out.println(Arrays.toString(arr));    }}

2、单边循环法

双边循环更加直观，但代码比较麻烦，而单边循环法从数列的一边对元素进行遍历交换。

开始循环选定基准元素p，再设置一个mark指针指向数列起始位置，mark代表着小于基准元素区域的右边界。

从基准元素的下一位开始遍历，若元素大于基准元素，则继续往后遍历。如果小于基准元素，先将mark指针右移一位，然后将最新遍历的元素与基准元素交换。

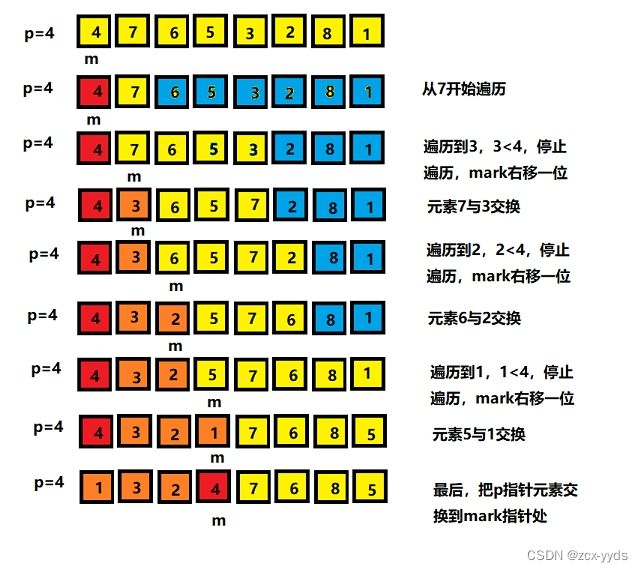
单边循环法与双边循环法主要是partition函数的实现不一样

    public static int partition(int arr[],int startIndex,int endIndex)    {        int p=arr[startIndex];//基准元素(可取随机位置)        int mark=startIndex;        for(int i=startIndex+1;i<=endIndex;i++){            if(arr[i]                mark++;                int tmp=arr[mark];                arr[mark]=arr[i];                arr[i]=tmp;            }        }        //交换基准元素和mark指针的元素        arr[startIndex]=arr[mark];        arr[mark]=p;        return mark;    }

可以看出，单边循环法只需要一个循环即可，比双边循环法要简单很多。

来源地址：https://blog.csdn.net/zcxyywd/article/details/131024516