人工智能高斯差分隐私框架与深度学习结合

人工智能中的隐私问题已经公认为一个重要并且严肃的问题。近日，宾夕法尼亚大学的研究组开发了一个新的数据隐私分析框架，可以在多个类型的机器学习问题中有效保护个人隐私。这个框架现已成功和深度学习结合，并在多个需要保障隐私的深度学习任务中达到最高准确率。

什么是差分隐私

在这个大数据时代，如何妥善获取和使用与真人相关的数据，渐渐成为迫切需要解决的问题。没有人希望自己生个病，上个网，买件衣服都会被人随意知晓，更别提手机里没有修过的自拍了。一种简单的隐私保护方法就是「匿名」：将收集到的数据中涉及个人信息的特征剔除。可惜这种方法并不可靠，曾有研究将 Netflix 匿名处理过的观影记录通过交叉对比 IMDb 数据库解匿成功，这直接导致了第二届 Netflix 数据分析大奖赛的取消。

2006 年，隐私算法的研究迎来了新的里程碑。Cynthia Dwork, Frank McSherry, Kobbi Nissim 和 Adam Smith 四位科学家定义了「差分隐私」（以下缩写为 DP），来严谨地分析隐私这个概念。差分隐私很快被证明是个强有效的工具，并被谷歌、苹果、微软、阿里巴巴等各大机构使用。而四位发明者于 2017 年获得了被誉为理论计算机科学界诺贝尔奖的 Godel 奖。

要理解差分隐私，我们可以看看下面这个简单的假设检验：假设有两个数据集 S, S'

S={小明，小刚，小美}；S'={小红，小刚，小美}

我们说这两个数据集是邻近的，因为它们的差异仅体现在一个人上。我们的目的是检验我们的模型是否是基于 S 训练的，这等价于检验小明是否存在于我们的数据中。如果这个假设检验非常困难，那么想要获取小明信息的攻击者就难以得逞。严谨来说，一个随机算法 M 符合 (epsilon,delta)-DP 意味着对于任何的事件 E,

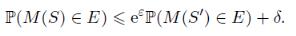
从定义不难看出，epsilon 和 delta 越小，隐私性越好。那么，如何实现能保证算法的隐私性呢?

具体做法是衡量算法的中间产物（比如梯度）的敏感性，并根据其大小施加一个成正比的噪音。由于噪音的存在，想要窃取小明信息的攻击者便无法确定小明是否在训练集中。在深度神经网络中，每一次迭代都会牺牲一部分隐私来换取性能的提高。我们可以对每个批（batch）的梯度加噪音，从而达到混淆攻击者的目的。

当然，噪音加的越大，隐私就越安全，但是随之性能也自然越差。在有限的隐私预算下，很多时候隐私算法的性能表现会不如人意。

深度学习经常需要敏感的个人信息来训练。现存的差分隐私定义以及隐私模型都试图在性能和隐私中找到一个平衡。可惜的是，这些尝试仍不能很好的处理两个重要环节：subsampling 和 composition。这导致了隐私算法的性能通常远逊于非隐私算法。

高斯差分隐私

Gaussian differential privacy (GDP) 是最近被提出的一种隐私表示方法。它可以精确的刻画 optimizer 在每个 epoch 所消耗的隐私。GDP 的表达简洁且是广义的（在 SGD, Adam, Adagrad 等多个优化器上的刻画是完全一样的）。GDP 的分析被进一步推广到 Poisson subsampling 和新的优化器上。新的推广得到了理论上严谨的证明，尤其证明了它优于此前最先进的 Moments accountant 方法。

在《Gaussian Differential Privacy》一文中，宾夕法尼亚大学的董金硕、Aaron Roth 和苏炜杰创新性地定义了「f-DP」来刻画隐私。如果用 alpha 来表示第一类错误，beta 来表示第二类错误，对于任何一种拒绝规则 (rejection rule) phi，都存在一个抵换函数 (trade-off function) T：降低第一类错误会导致第二类错误增加，反之亦然。我们将两类错误的和的最小值称为最小错误和。

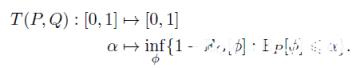
一个随机算法 M 在 S 和 S』上的抵换函数 T 如果始终大于函数 f，那么它就满足 f-DP。

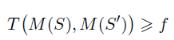
对比于传统的 eps,delta-DP，f-DP 使用的是一个函数 f，这也使得其刻画更为自由和准确。

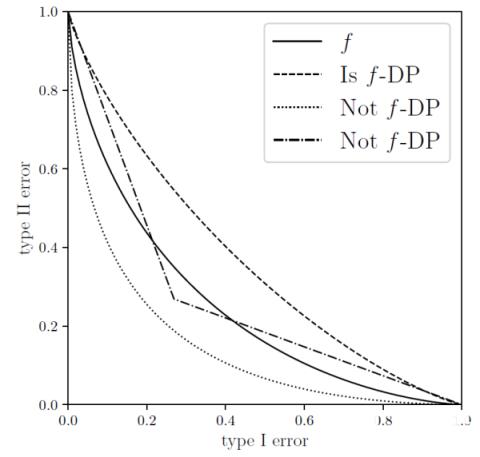
作为 f-DP 的一个重要案例，作者随后介绍了高斯差分隐私（GDP）来区分两个高斯分布。根据中心极限定理（CLT），任何基于假设检验的隐私定义在极限情况下都会收敛于 GDP。事实上，相对于谷歌在 2016 年提出的，适用于计算 epsilon,delta-DP 的 Moments Accountant (MA) 方法，本文提出的 CLT 方法可以更简易地计算 GDP，而且非常准确。值得注意的是，该文章最近被国际顶级统计学杂志 Journal of the Royal Statistical Society: Series B 接收为 Discussion paper，这是数据科学界对该工作的一种认可。

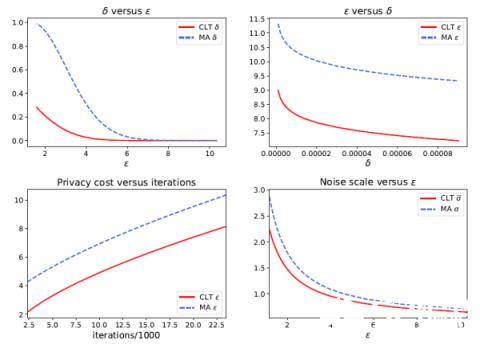
GDP 与深度学习的结合

GDP 的好处还不止于此。在最新工作《Deep Learning with Gaussian Differential Privacy》中，卜至祺、董金硕，龙琦和苏炜杰等作者指出 GDP 和 eps,delta-DP 可以通过他们设计的 Dual 函数互相转换。也就是说，研究者可以在 f-DP 的框架下分析算法再转成传统的 dp，或者从传统领域中拿来已有的理论和技巧，不必二次开发。这项技术现在已经在 TensorFlow 中实现。

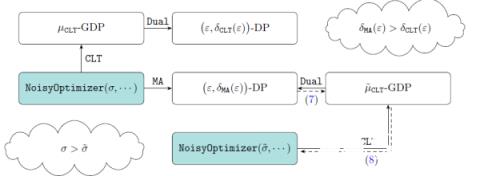
• 论文地址：https://arxiv.org/abs/1911.11607
• 项目实现：https://github.com/tensorflow/privacy/blob/master/tensorflow_privacy/privacy/analysis/gdp_accountant.py

在实验中，作者们将 GDP 和深度学习结合，并在多种类型的任务上取得了不俗的成绩。此前谷歌也曾将 epsDP 和深度学习结合，虽然在 MNIST 图像识别上取得了 97% 的正确率（无隐私算法可达到 99% 以上），在 CIFAR10 上却止步于 73% 的正确率（无隐私算法可达 86%）。而利用 GDP 的精确刻画，作者们在 MNIST 上取得了 98% 的准确率。不仅如此，MA 计算的结果表示 MNIST 的 96.6% 正确率对应的是 9.4% 的最小错误和，意味着攻击者有超过九成的概率猜对一张图片是否在数据集中。而 CLT 的计算表明 epsDP 太过于保守：同样的模型同样的表现，实际对应的最小错误和其实是 77.6%，也就是说隐私并没有损失很多。

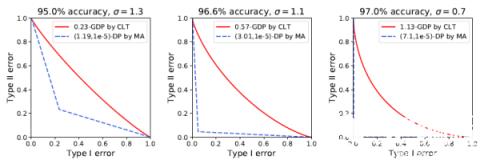
为了全面探讨 GDP 的优越性，作者在 GDP 框架下分析了神经网络的表现。作者实现了 SGD 和 Adam 的隐私版本，并通过让神经网络不断迭代直到 GDP 达到了 mu=2。在 IMDb（自然语言处理），MovieLens 1M（推荐系统）和 Adult Income（非图像型分类任务）上，GDP 模型都取得了非常接近无隐私模型的性能。例如在 Adult Income 数据上，隐私神经网络和无隐私神经网络表现几乎一样好，意味着隐私也许并不需要以很大的性能牺牲为代价。更进一步的，作者强调文中的神经网络都相对简单（不超过三层），如果使用更复杂更高级的神经网络可以在同样的隐私保证下更显著地提升性能。而另一方面，使用高效的优化算法（减少迭代次数，即隐私的损失次数）也能让性能变得更好。

既然 CLT 可以在同样性能的条件下比 MA 更好地保护隐私，那么反过来想，在同样的隐私预算下，GDP 也能显示出更强的性能。作者构思了一个实验来说明这一点：训练一个加了 sigma 噪音的神经网络若干步，通过 MA 可以算出目前损失了多少隐私，通过 CLT 和 Dual 反解出真正必须的噪音 sigma hat。注意 sigma hat 必然小于 sigma，然后训练同一个神经网络但只加 sigma hat 噪音。由于噪音变小，新的神经网络学习效果会更好，而且在每一次迭代，新神经网络都会更好地保护隐私。

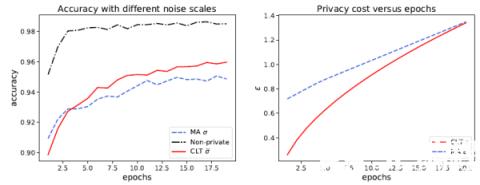
将神经网络和 GDP 结合，可以更精准地呈现隐私损失，从而更好地保护隐私以及提升隐私算法的性能。另一方面，已有的 (epsilon,delta)-DP 研究也可以嫁接到 GDP 中，为两个领域带来了新的机遇。这一隐私算法领域的新进展给予了研究者们更大的信心去相信，随着机器学习的进一步发展，我们也许在不远的未来就能以可忽略不计的代价来保护我们的隐私。同时，它也鼓励人们更愿意分享涉及个人信息的数据，来推动机器学习的发展。

人工智能可以对人的意识、思维的信息过程的模拟。 人工智能是一门极富挑战性的科学，从事这项工作的人必须懂得计算机知识，心理学和哲学。