今天小编给大家分享一下pytorch怎么定义新的自动求导函数的相关知识点,内容详细,逻辑清晰,相信大部分人都还太了解这方面的知识,所以分享这篇文章给大家参考一下,希望大家阅读完这篇文章后有所收获,下面我们一起来了解一下吧。
pytorch定义新的自动求导函数
在pytorch中想自定义求导函数,通过实现torch.autograd.Function并重写forward和backward函数,来定义自己的自动求导运算。
直接上代码,定义一个ReLu来实现自动求导
import torchclass MyRelu(torch.autograd.Function): @staticmethod def forward(ctx, input): # 我们使用ctx上下文对象来缓存,以便在反向传播中使用,ctx存储时候只能存tensor # 在正向传播中,我们接收一个上下文对象ctx和一个包含输入的张量input; # 我们必须返回一个包含输出的张量, # input.clamp(min = 0)表示讲输入中所有值范围规定到0到正无穷,如input=[-1,-2,3]则被转换成input=[0,0,3] ctx.save_for_backward(input) # 返回几个值,backward接受参数则包含ctx和这几个值 return input.clamp(min = 0) @staticmethod def backward(ctx, grad_output): # 把ctx中存储的input张量读取出来 input, = ctx.saved_tensors # grad_output存放反向传播过程中的梯度 grad_input = grad_output.clone() # 这儿就是ReLu的规则,表示原始数据小于0,则relu为0,因此对应索引的梯度都置为0 grad_input[input < 0] = 0 return grad_input进行输入数据并测试
dtype = torch.floatdevice = torch.device('cuda' if torch.cuda.is_available() else 'cpu')# 使用torch的generator定义随机数,注意产生的是cpu随机数还是gpu随机数generator=torch.Generator(device).manual_seed(42)# N是Batch, H is hidden dimension,# D_in is input dimension;D_out is output dimension.N, D_in, H, D_out = 64, 1000, 100, 10x = torch.randn(N, D_in, device=device, dtype=dtype,generator=generator)y = torch.randn(N, D_out, device=device, dtype=dtype, generator=generator)w1 = torch.randn(D_in, H, device=device, dtype=dtype, requires_grad=True, generator=generator)w2 = torch.randn(H, D_out, device=device, dtype=dtype, requires_grad=True, generator=generator)learning_rate = 1e-6for t in range(500): relu = MyRelu.apply # 使用函数传入参数运算 y_pred = relu(x.mm(w1)).mm(w2)# 计算损失 loss = (y_pred - y).pow(2).sum() if t % 100 == 99: print(t, loss.item()) # 传播 loss.backward() with torch.no_grad(): w1 -= learning_rate * w1.grad w2 -= learning_rate * w2.grad w1.grad.zero_() w2.grad.zero_()pytorch自动求导与逻辑回归
自动求导
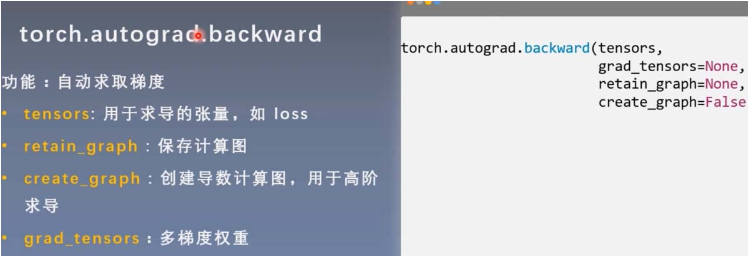
retain_graph设为True,可以进行两次反向传播
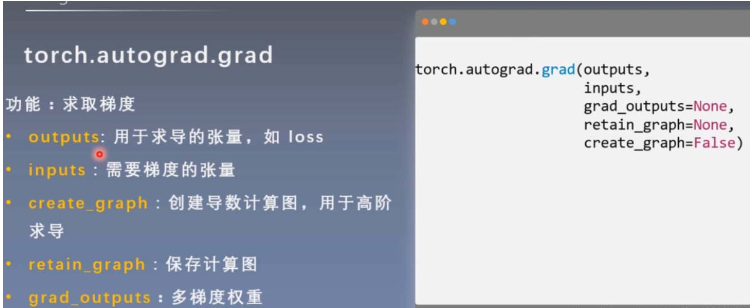

逻辑回归

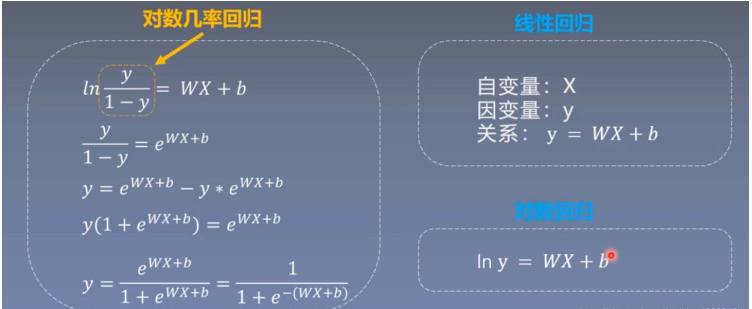
import torchimport torch.nn as nnimport matplotlib.pyplot as pltimport numpy as nptorch.manual_seed(10)#========生成数据=============sample_nums = 100mean_value = 1.7bias = 1n_data = torch.ones(sample_nums,2)x0 = torch.normal(mean_value*n_data,1)+bias#类别0数据y0 = torch.zeros(sample_nums)#类别0标签x1 = torch.normal(-mean_value*n_data,1)+bias#类别1数据y1 = torch.ones(sample_nums)#类别1标签train_x = torch.cat((x0,x1),0)train_y = torch.cat((y0,y1),0)#==========选择模型===========class LR(nn.Module): def __init__(self): super(LR,self).__init__() self.features = nn.Linear(2,1) self.sigmoid = nn.Sigmoid() def forward(self,x): x = self.features(x) x = self.sigmoid(x) return xlr_net = LR()#实例化逻辑回归模型#==============选择损失函数===============loss_fn = nn.BCELoss()#==============选择优化器=================lr = 0.01optimizer = torch.optim.SGD(lr_net.parameters(),lr = lr,momentum=0.9)#===============模型训练==================for iteration in range(1000): #前向传播 y_pred = lr_net(train_x)#模型的输出 #计算loss loss = loss_fn(y_pred.squeeze(),train_y) #反向传播 loss.backward() #更新参数 optimizer.step() #绘图 if iteration % 20 == 0: mask = y_pred.ge(0.5).float().squeeze() #以0.5分类 correct = (mask==train_y).sum()#正确预测样本数 acc = correct.item()/train_y.size(0)#分类准确率 plt.scatter(x0.data.numpy()[:,0],x0.data.numpy()[:,1],c='r',label='class0') plt.scatter(x1.data.numpy()[:,0],x1.data.numpy()[:,1],c='b',label='class1') w0,w1 = lr_net.features.weight[0] w0,w1 = float(w0.item()),float(w1.item()) plot_b = float(lr_net.features.bias[0].item()) plot_x = np.arange(-6,6,0.1) plot_y = (-w0*plot_x-plot_b)/w1 plt.xlim(-5,7) plt.ylim(-7,7) plt.plot(plot_x,plot_y) plt.text(-5,5,'Loss=%.4f'%loss.data.numpy(),fontdict={'size':20,'color':'red'}) plt.title('Iteration:{}\nw0:{:.2f} w1:{:.2f} b{:.2f} accuracy:{:2%}'.format(iteration,w0,w1,plot_b,acc)) plt.legend() plt.show() plt.pause(0.5) if acc > 0.99: break以上就是“pytorch怎么定义新的自动求导函数”这篇文章的所有内容,感谢各位的阅读!相信大家阅读完这篇文章都有很大的收获,小编每天都会为大家更新不同的知识,如果还想学习更多的知识,请关注编程网行业资讯频道。








