【数据结构与算法】如何对快速排序进行细节优化以及实现非递归版本的快速排序？

君兮_的个人主页

即使走的再远，也勿忘启程时的初心

C/C++ 游戏开发

Hello,米娜桑们，这里是君兮_，国庆长假结束了，无论是工作还是学习都该回到正轨上来了，从今天开始恢复正常的更新频率，今天为大家带来的内容是快速排序的两大优化和非递归实现

• 好了废话不多说，开始我们今天的学习吧！！
  

  快排优化与非递归实现

  • 快速排序优化
  • • 三数去中优化
    • 对递归次数的优化
  • 非递归的快速排序
  • 总结

快速排序优化

• 有关快速排序的基本内容可以去看看这篇博客，讲的已经非常详细了
  【算法速查】万字图解带你快速入门八大排序(下）
• 我们在这里就以hoare版本的快速排序来讲讲还可以优化的地方以及为什么
• hoare版本的快速排序代码如下：

Swap(int* p1, int* p2){    int tmp = *p1;    *p1 = *p2;    *p2 = tmp;}int getMid(int* a, int left, int right){    assert(a);    int mid = (left + right) / 2;    if (a[left] > a[mid])    {        if (a[mid] > a[right])            return mid;        else if(a[right]>a[left])        {            return left;        }        else        {            return right;        }    }    else    {        if (a[mid] < a[right])            return mid;        else if (a[left] > a[right])        {            return left;        }        else        {            return right;        }    }}int PartSort1(int* a, int left, int right){    int mid = getMid(a, left, right);//三数取中    //把取好的key放到left中    Swap(&a[left], &a[mid]);    int key = left;    while (left<right)    {    //右边先走        while (left < right && a[right] >= a[key])        {            right--;        }      //左边走        while (left<right&&a[left]<=a[key])        {            left++;        }        //交换        Swap(&a[left], &a[right]);    }    //交换停下的位置的值把key换到此时左右相遇的位置    Swap(&a[key], &a[left]);    //此时key的左右都有序，由于right，left都指处于key的位置返回任意即可    return right;}void QuickSort(int* a, int left,int right){//只剩下一个值了，说明已经有序，不需要再排，递归结束    if (left >= right)        return;       int key = PartSort1(a,left,right);    //key已经满足左右都有序了不需要再排    //排key的左边    QuickSort(a, left, key-1);    //排key的右边    QuickSort(a, key+1, right);}

三数去中优化

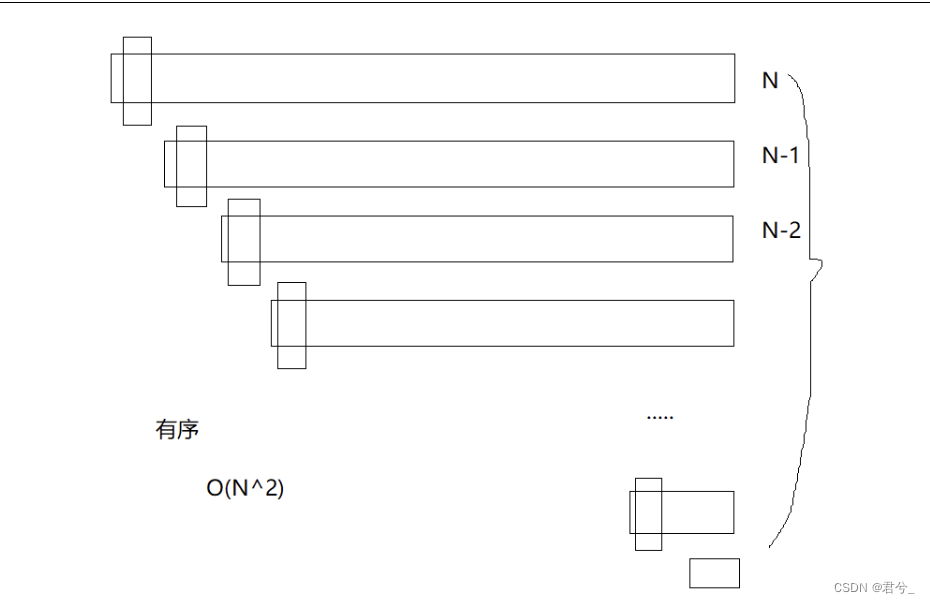
• 我们知道，快速排序是先取一个key值然后让左右两边有序来进行排序的，因此key值的取值对我们快速排序的速度是有比较大的影响的，举个最坏的例子，假设每次我们取到的key值都是此次所需排序数据中最小的，如下图所示
  

• 此时的时间复杂度就是O(N^2)了，因此，我们需要对快速排序进行优化，尽量减少出现图示的这种情况，就有了以下的代码

int getMid(int* a, int left, int right){    assert(a);    int mid = (left + right) / 2;    if (a[left] > a[mid])    {        if (a[mid] > a[right])            return mid;        else if(a[right]>a[left])        {            return left;        }        else        {            return right;        }    }    else    {        if (a[mid] < a[right])            return mid;        else if (a[left] > a[right])        {            return left;        }        else        {            return right;        }    }}

• 简单的来说，上述这段代码表示的是这样的意思
  取最左，最右，中间三个数，分别对三个数进行比较，最终取得的值就是处于三个值中中间的这个值。
• 通过上述这个优化，此时所需排序的数据中总要比我们取得的key值小以及比我们取得的key值大的值存在，就能较大的提供我们的快排效率啦！

对递归次数的优化

• 我们在使用递归版本的快速排序时，当区间中的数比较少时，仍然使用递归的方式进行是会消耗非常多不必要消耗的内存的，还是举个例子：假设此时区间中还有10个数需要排
  
• 我们递归返回的条件是left>=right,递归是栈中开辟空间进行的，当递归的层数过深，栈的大小又不是很大，就容易造成“爆栈”，如上图所示，为了排序这十个数，我们又递归了这么多层，是非常不明智的选择，因此，我们在数据较少的情况出现时，可以使用插入排序等方法进行排序，减少不必要的空间浪费，也能提供我们快排的速度

void QuickSort1(int* a, int begin, int end){if (begin >= end)return;// 小区间优化，小区间不再递归分割排序，降低递归次数if ((end - begin + 1) > 10){int keyi = PartSort1(a, begin, end);// [begin, keyi-1] keyi [keyi+1, end]QuickSort1(a, begin, keyi - 1);QuickSort1(a, keyi + 1, end);}else{InsertSort(a + begin, end - begin + 1);}}

• 好了，讲完了上述对递归版本的快排优化，接下来我们讲讲快速排序的非递归版本

非递归的快速排序

• 我们上面讲了，递归是在栈空间中进行的，栈空间又比较小，当递归层数比较深时就会造成“爆栈”，因此对于快速排序这种我们常用的排序算法来说，掌握其非递归版本也是非常重要的
• 想要了解非递归，我们就必须从递归开始下手，我们再来看看递归的这段代码

void QuickSort1(int* a, int begin, int end){if (begin >= end)return;// 小区间优化，小区间不再递归分割排序，降低递归次数if ((end - begin + 1) > 10){int keyi = PartSort1(a, begin, end);// [begin, keyi-1] keyi [keyi+1, end]QuickSort1(a, begin, keyi - 1);QuickSort1(a, keyi + 1, end);}else{InsertSort(a + begin, end - begin + 1);}}

• 如果你学过数据结构的话，会发现我们递归与栈是非常类似的，栈是后进先出，最后再处理最先放入的，而递归也是先往深处走，再往回返，因此，我们在实现非递归的快速排序时，选用栈这种数据结构来帮助我们进行。

void QuickSortNonR(int* a, int left,int right){    Stack st;    StackInit(&st);//初始化栈    StackPush(&st, left);//入栈    StackPush(&st, right);    while (!StackEmpty(&st))//判断栈是否为空    {        int right = StackTop(&st);//后进先出，取栈顶元素        StackPop(&st);//此时的栈顶元素出栈        int left = StackTop(&st);//此时的栈顶为left        StackPop(&st);        int key = PartSort1(a, left, right);//选key值        if (key + 1 < right)//此时key+1小于right 把key+1作为下一次排序的左 right作为右入栈        {            StackPush(&st, key + 1);            StackPush(&st, right);        }        if (left < key - 1)//key-1大于left key-1就为下一次循环的右，left为左        {            StackPush(&st, left);            StackPush(&st, key - 1);        }    }    //当栈中没有元素了，说明此时的左大于等于右，此时已经没有数据未进行排序了    StackDestroy(&st);//销毁栈}

• 和递归大致是一样的，只不过我们是用栈的方式来模拟递归朝深度进行，如果你能理解递归实现的快速排序，相信非递归实现的快速排序对你来说也非常好理解
• 唯一需要注意的是入栈和出栈的顺序，当你开始先入右再入左的话，由于后进先出的原因，先出的是左其中是右，这点在取栈顶元素作为排序的左右区间时一定要注意避免取错。

总结

• 好啦，我们总算把八大排序算法都讲完了，算法这一块光靠看代码不是那么容易理解的，因此我花了大量的时间画图分析，希望能对你有所帮助
• 当然，这篇文章创作的初衷是希望帮助初学者对排序算法有一个大致的了解，对已经学过的人起到在需要使用的时候快速回忆的效果，因此可能还有一部分细节不全，之后我会挑出重点单独出博客讲解
• 有任何的问题和对文章内容的疑惑欢迎在评论区中提出，当然也可以私信我，我会在第一时间回复的！！

新人博主创作不易，如果感觉文章内容对你有所帮助的话不妨三连一下再走呗。你们的支持就是我更新的动力！！！

**（可莉请求你们三连支持一下博主！！！点击下方评论点赞收藏帮帮可莉吧）**

来源地址：https://blog.csdn.net/syf666250/article/details/133691828