这篇文章主要介绍“Python在画图时怎么使用特殊符号”的相关知识,小编通过实际案例向大家展示操作过程,操作方法简单快捷,实用性强,希望这篇“Python在画图时怎么使用特殊符号”文章能帮助大家解决问题。
一、问题背景
在论文中,如何使用特殊符号进行表示?这里给出效果图和代码
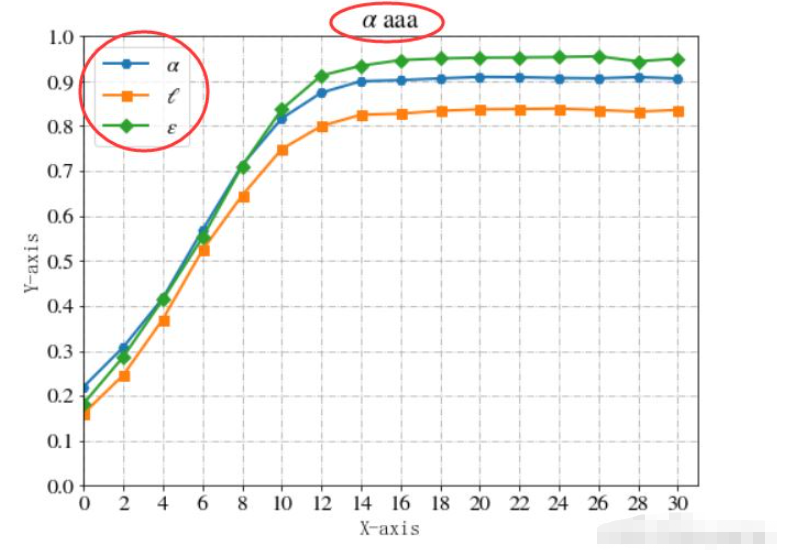
完整代码:
from matplotlib import pyplotimport matplotlib.pyplot as pltfrom matplotlib.font_manager import FontPropertiesfrom matplotlib.ticker import MultipleLocator, FormatStrFormatter font_set = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=15)import matplotlibimport numpy as npfrom mpl_toolkits.axes_grid1.inset_locator import inset_axesfrom mpl_toolkits.axes_grid1.inset_locator import mark_insetfrom matplotlib.patches import ConnectionPatch%matplotlib inlineplt.rcParams['figure.figsize'] = (8.0, 6.0) # set default size of plotsplt.rcParams['image.interpolation'] = 'nearest'plt.rcParams['image.cmap'] = 'gray'plt.rcParams['font.sans-serif']=['SimHei']plt.rcParams['axes.unicode_minus']=False # 设置大小plt.rcParams['font.size'] = '16'#解决画多幅图时出现图形部分重叠fig = plt.figure()matplotlib.rcParams.update({'text.usetex': False,'font.family': 'stixgeneral','mathtext.fontset': 'stix',})myfont = FontProperties(fname='/home/linuxidc/.local/share/fonts/文泉驿正黑.ttf')#准备数据x = range(0,31,2)A=[0.2204262385828951,0.30839304560351055,0.4176158354528364,0.5689115113547377,0.7132088021728286,0.8170438670019559,0.874248496993988,0.8998229892687244,0.9022254048694502,0.9059819476369345,0.9094392004441977,0.9087585175336547,0.9070491438736936,0.9061997894620201,0.9090201312423535,0.905820399113082]B=[0.16086354829781346,0.24623673832139087,0.37067344907663385,0.5243875153820338,0.6455296269608115,0.7488125174629785,0.8000445335114674,0.8252572187188848,0.8275862068965517,0.8340528115714526,0.8372015546918379,0.837903717245582,0.8390037802979764,0.8358911851072082,0.8319986653319986,0.8359756097560975]C=[0.18306116800442845,0.2870632672332389,0.4144089350879133,0.5520192415258978,0.7109362008757829,0.8372170997485331,0.9124159429971054,0.9341066489655936,0.946792993279718,0.9503133935078769,0.9521488062187674,0.952635311063099,0.9535668223259951,0.9552372984652889,0.9439895451006562,0.9501552106430155]#绘图fig, ax = plt.subplots(1, 1)ax.plot(x, A, marker='H',linewidth=2,markersize=7,label=r'$\alpha$')ax.plot(x, B, marker='s',linewidth=2,markersize=7,label=r'$\ell$')ax.plot(x, C, marker='D',linewidth=2,markersize=7,label=r'$\mu$')plt.grid(linestyle='-.') plt.grid(True)y_major_locator=MultipleLocator(0.1)x_major_locator=MultipleLocator(2)ax=plt.gca()ax.xaxis.set_major_locator(x_major_locator)ax.yaxis.set_major_locator(y_major_locator)plt.ylim(0,1.0)plt.xlim(0,31)plt.legend() # 让图例生效plt.title(r'$\alpha$ aaa')plt.xlabel('X-axis',fontproperties=font_set) #X轴标签plt.ylabel("Y-axis",fontproperties=font_set) #Y轴标签plt.grid(linestyle='-.') plt.show()二、注意事项
应用例子,可以在(title)、坐标轴名(xlabel、ylabel)、标注标签处(label)增加。注意使用label等号后面使用“r”,否则直接报错。
以此为例进行替换即可↓
ax.plot(x, A, marker='H',linewidth=2,markersize=7,label=r'$\alpha$')三、常见特殊符号及对应代码
| 符号 | α | β | δ | ℓ | ε |
| 代码 | $\alpha$ | $\beta$ | $\delta$ | $\ell$ | $\varepsilon$ |
| 符号 | Φ | γ | η | ι | φ |
| 代码 | $\phi $ | $\gamma$ | $\eta$ | $\iota$ | $\varphi$ |
| 符号 | λ | μ | π | θ | ρ |
| 代码 | $\lambda$ | $\mu$ | $\pi$ | $\theta$ | $\rho$ |
| 符号 | σ | τ | ω | ξ | Γ |
| 代码 | $\sigma$ | $\tau$ | $\omega$ | $\xi$ | $\Gamma$ |
四、引入特殊符号的万能方法
那么肯定有人要问了,如果要表达的字符很复杂怎么办,比如带公式的。
事实上,这里有个通用方式。但是需要安装MathType。该方法在外文文献的Latex排版中也同样适用。
简单三步如下,:
①下载mathtype,并关联word

②打入你的表达式,编辑并复制
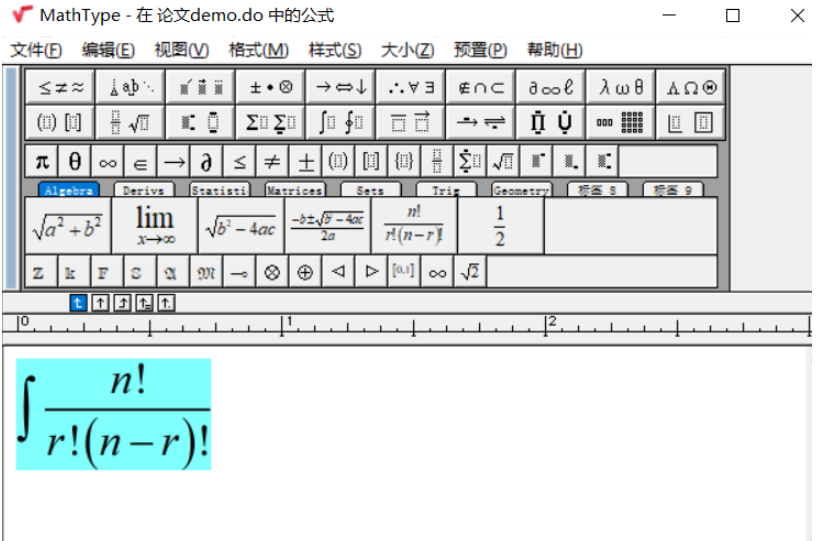
③在word输入位置黏贴

只需关注最后一行的
\[\int {\frac{{n!}}{{r!\left( {n - r} \right)!}}} \]去掉两边的“\[”和“\]”
保留结果为
\int {\frac{{n!}}{{r!\left( {n - r} \right)!}}}调用的时候两边加上$即可
ax.plot(x, C, marker='D',linewidth=2,markersize=7,label=r'$\int {\frac{{n!}}{{r!\left( {n - r} \right)!}}} $')效果如下:
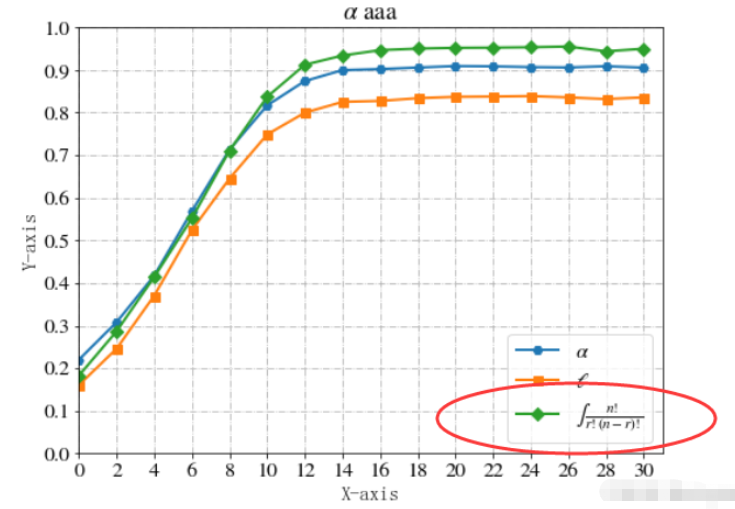
关于“Python在画图时怎么使用特殊符号”的内容就介绍到这里了,感谢大家的阅读。如果想了解更多行业相关的知识,可以关注编程网行业资讯频道,小编每天都会为大家更新不同的知识点。






