一、相关分析
(1)衡量事物之间或称变量之间线性相关程度的强弱,并用适当的统计指标表示出来的过程。
(2)比如家庭收入和支出、一个人所受教育程度与其收入、子女身高和父母身高的相关性。
二、相关系数
(1)衡量变量之间相关程度的一个量值。
(2)相关系数r的数值范围是在-1到+1之间。
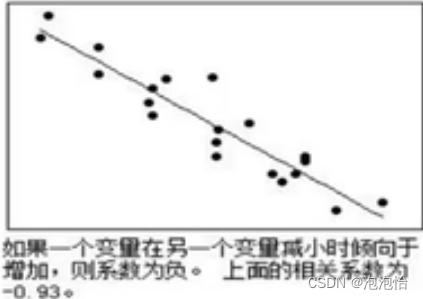
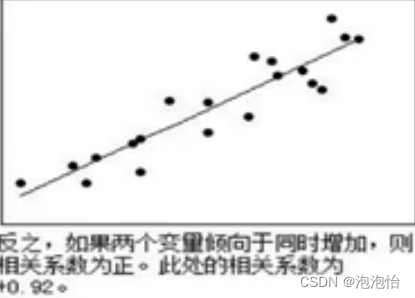
(3)相关系数r的正负号表示变化方向。(“+”号表示变化方向一致,“-”号表示变化方向相反)
举个例子:当父母身高越高子女身高越高,这呈现的是正相关;当父母身高越高子女身高越低,这呈现的是负相关。
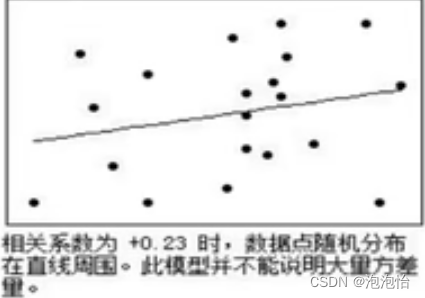
(4)r的绝对值表示变量之间的密切程度(即强度)。绝对值越接近1,表示两个变量之间关系越密切;越接近零,表示两个变量之间关系越不密切。
(5)相关系数的值,仅仅是一个比值。它不是由相单位度量而来(即不等距),也不是百分比,因此,不能直接作加、减、乘、除运算。
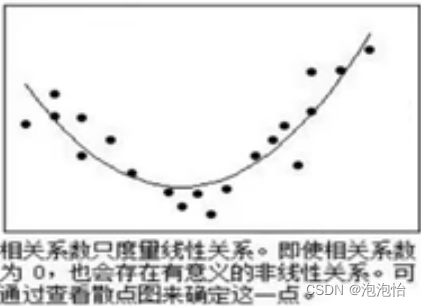
(6)相关系数只能描述两个变量之间的变化方向及密切程度,并不能揭示二者之间的内在本质联系,即存在相关的两个变量,不一定存在因果关系。
三、连续变量的相关分析
(1)连续变量即数据变量,它的取值之间可以比较大小,可以用加减法计算出差异的大小。如“年龄”、“收入”、“成绩”等变量。
(2)当两个变量都是正态连续变量,而且两者之间呈线性关系时,通常用Pearson相关系数来衡量。
四、Pearson相关系数
(1)协方差:
协方差是一个反应两个随机变量相关程度的指标,如果一个变量跟随着另一个变量同时变大或者变小,那么这两个变量的协方差就是正值。
(2)公式:
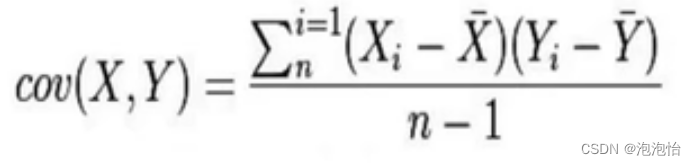
虽然协方差能反映两个随机变量的相关程度(协方差大于零表示两者正相关,小于零表示两者负相关),但是协方差值的大小并不能很好的度量两个随机变量的关联程度。
在二维空间中分布着一些数据,我们知道数据点坐标X轴·Y轴的相关程度,如果X与·Y
的相关性较小但数据分布的比较离散,这样会导致求出的协方差值较大,用这个度量相关程度是不合理的,因此捏,引入Pearson相关系数,在原来基础上除以两个随机变量的标准差。
(3)皮尔森相关系数公式:
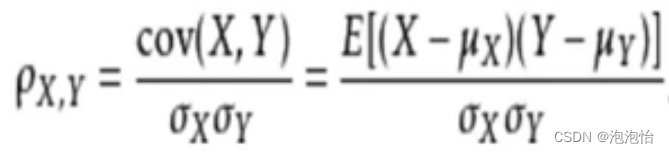
(4)np.corrcoef(a)可计算行与行之间的相关系数。np.corrcoef(a,rowvar=0)用于计算各列之间的相关系数。
代码:
import numpy as nppaopao=np.array([ [10,10,8,9,7], [4,5,4,3,3], [3,3,1,1,1]])print(paopao)print(np.corrcoef(paopao))np.corrcoef((paopao),rowvar=0)结果加解释: (对称矩阵哈)

五、相关系数的显著性检验
假设: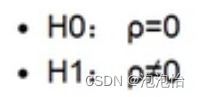
统计量: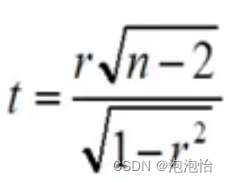
计算出来t看其是否落在拒绝域内,进行判断。
代码:
import scipy.stats as statsimport scipyx=[10.35,6.24,3.18,8.46,3.21,7.65,4.32,8.66,9.12,10.31]y=[5.1,3.15,1.67,4.33,1.76,4.11,2.11,4.88,4.99,5.12]correlation,pvalue=stats.stats.pearsonr(x,y)print('correlation:',correlation)print('pvalue:',pvalue)结果:

看出远小于所以落在了接受域内。
来源地址:https://blog.csdn.net/m0_72662900/article/details/127651823




