【机器学习】DBSCAN聚类算法（含Python实现）

文章目录

• 一、算法介绍
• 二、例子
• 三、Python实现
• • 3.1 例1
  • 3.2 算法参数详解
  • 3.3 鸢尾花数据集

一、算法介绍

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）是一种基于密度的聚类算法，可以将数据点分成不同的簇，并且能够识别噪声点（不属于任何簇的点）。

DBSCAN聚类算法的基本思想是：

在给定的数据集中，根据每个数据点周围其他数据点的密度情况，将数据点分为核心点、边界点和噪声点。

• 核心点是周围某个半径内有足够多其他数据点的数据点；
• 边界点是不满足核心点要求，但在某个核心点的半径内的数据点；
• 噪声点则是不满足任何条件的点。

接着，从核心点开始，通过密度相连的数据点不断扩张，形成一个簇。

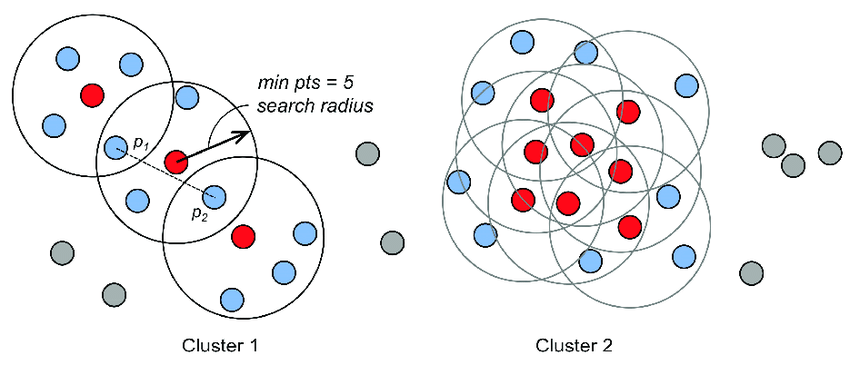
DBSCAN算法的优点是能够处理任意形状的簇，不需要先预先指定簇的个数，能够自动识别噪声点并将其排除在聚类之外。

然而，该算法的缺点是对于密度差异较大的数据集，可能无法有效聚类。此外，算法的参数需要根据数据集的特性来合理选择，如半径参数和密度参数。

二、例子

假设我们有以下的数据点集合：

[(1,1), (1,2), (2,1), (8,8), (8,9), (9,8), (15,15)]

我们可以使用DBSCAN算法来将这些点分成不同的簇。

首先，我们需要设置两个参数：

• 半径$ϵ$
• 最小样本数$minPts$

我们这里设置$ϵ=2$，$minPts=3$。

接下来，我们从数据集中选取一个点，比如第一个点$(1,1)$作为种子点，并将该点标记为“核心点”，因为它周围有超过$minPts$个点在半径$ϵ$的范围内。

然后，我们找到与该点距离在$ϵ$内的所有点，将它们标记为与该点“密度直达”（density-reachable），并将这些点加入到同一个簇内。这里包括（1，2）和（2，1）。

接着，我们选取下一个未被分类的点，这里是（8，8），将其标记为“核心点”，并将与它距离在$ϵ$内的所有点加入同一簇中，这里包括（8，9）和（9，8）。

最后，我们选取最后一个未被分类的点，（15，15），但该点只有一个点在$ϵ$内，不足以满足$minPts$的要求，因此该点被标记为噪声点。

于是，最终的聚类结果为：

Cluster 1: [(1,1), (1,2), (2,1)]Cluster 2: [(8,8), (8,9), (9,8)]Noise: [(15,15)]

可以看出，DBSCAN算法成功地将数据点分成了两个簇，并且将噪声点（15，15）排除在聚类之外。

三、Python实现

3.1 例1

我们还是以上面例子为例，进行Python实现：

from sklearn.cluster import DBSCANimport numpy as np# 输入数据X = np.array([(1,1), (1,2), (2,1), (8,8), (8,9), (9,8), (15,15)])# 创建DBSCAN对象，设置半径和最小样本数dbscan = DBSCAN(eps=2, min_samples=3)# 进行聚类labels = dbscan.fit_predict(X)# 输出聚类结果for i in range(max(labels)+1):    print(f"Cluster {i+1}: {list(X[labels==i])}")print(f"Noise: {list(X[labels==-1])}")

与手算结果一致。

我们使用chatgpt对上面的代码翻译一下：

这表明DBSCAN算法已经在输入数据中识别出了三个簇，第一个簇有三个点，第二个簇有三个点，第三个簇有一个点。在这个特定的数据集中没有噪声。

3.2 算法参数详解

下面对sklearn.cluster模块中的参数进行说明：

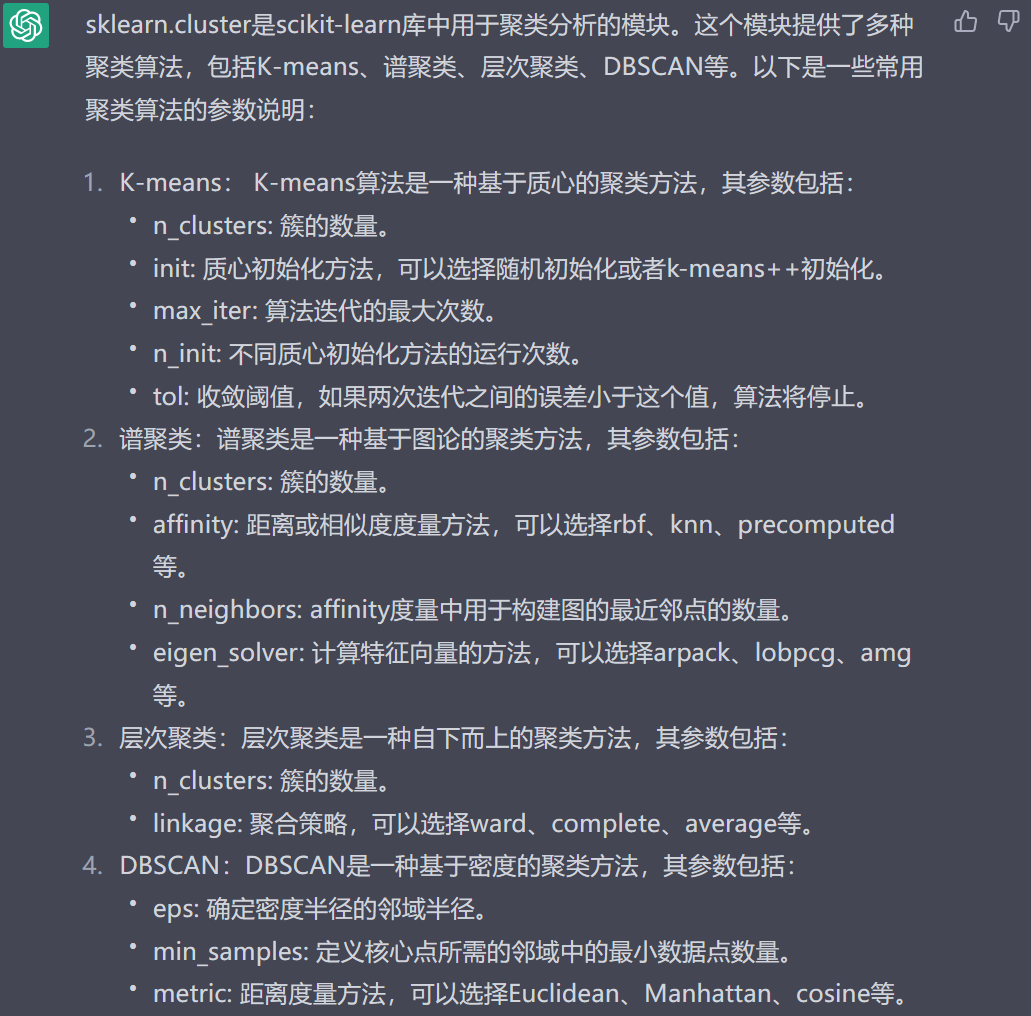
总之，不同的聚类算法具有不同的参数设置，可以根据具体问题选择不同的算法和参数组合来实现最佳的聚类效果。

DBSCAN算法的调用方法如下：

DBSCAN(eps=0.5, *, min_samples=5, metric='euclidean', metric_params=None, algorithm='auto', leaf_size=30, p=None, n_jobs=None)

该算法提供了多个可调参数，以控制算法的聚类效果。下面对常用的参数进行详细说明：

• eps：控制着半径的大小，是判断两个数据点是否属于同一簇的距离阈值。默认值为0.5。
• min_samples: 控制着核心点周围所需的最小数据点数。默认值为5。
• metric: 用于计算距离的度量方法，可以选择的方法包括欧式距离(euclidean)、曼哈顿距离(manhattan)等。默认值为欧式距离。
• algorithm: 用于计算距离的算法，可以选择的算法包括Ball Tree(ball_tree)、KD Tree(kd_tree)和brute force(brute)。Ball Tree和KD Tree算法适用于高维数据，brute force算法适用于低维数据。默认值为auto，自动选择算法。
• leaf_size: 如果使用Ball Tree或KD Tree算法，这个参数指定叶子节点的大小。默认值为30。
• p: 如果使用曼哈顿距离或闵可夫斯基距离(minkowski)，这个参数指定曼哈顿距离的p值。默认值为2，即欧式距离。
• n_jobs: 指定并行运算的CPU数量。默认值为1，表示单CPU运算。如果为-1，则使用所有可用的CPU。
• metric_params: 如果使用某些度量方法需要设置额外的参数，可以通过这个参数传递这些参数。默认值为None。

这些参数对于控制DBSCAN算法的聚类效果非常重要，需要根据具体的数据集和需求进行选择和调整。在使用DBSCAN算法时，我们通常需要对这些参数进行多次实验和调整，以达到最佳的聚类效果。

3.3 鸢尾花数据集

再以著名的鸢尾花数据集为例进行Python实现：

from sklearn.cluster import DBSCANfrom sklearn.datasets import load_irisfrom sklearn.preprocessing import StandardScaler# 加载数据集iris = load_iris()X = iris.data# 数据预处理，标准化数据scaler = StandardScaler()X = scaler.fit_transform(X)# 使用DBSCAN聚类算法dbscan = DBSCAN(eps=0.5, min_samples=5)y_pred = dbscan.fit_predict(X)# 输出聚类结果print('聚类结果:', y_pred)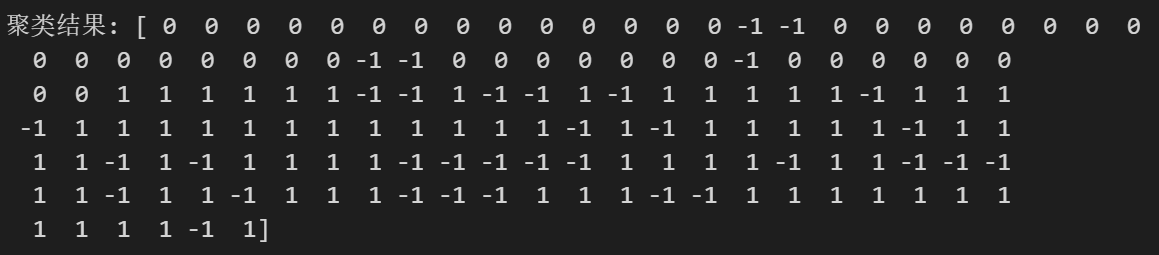

代码解释如下：

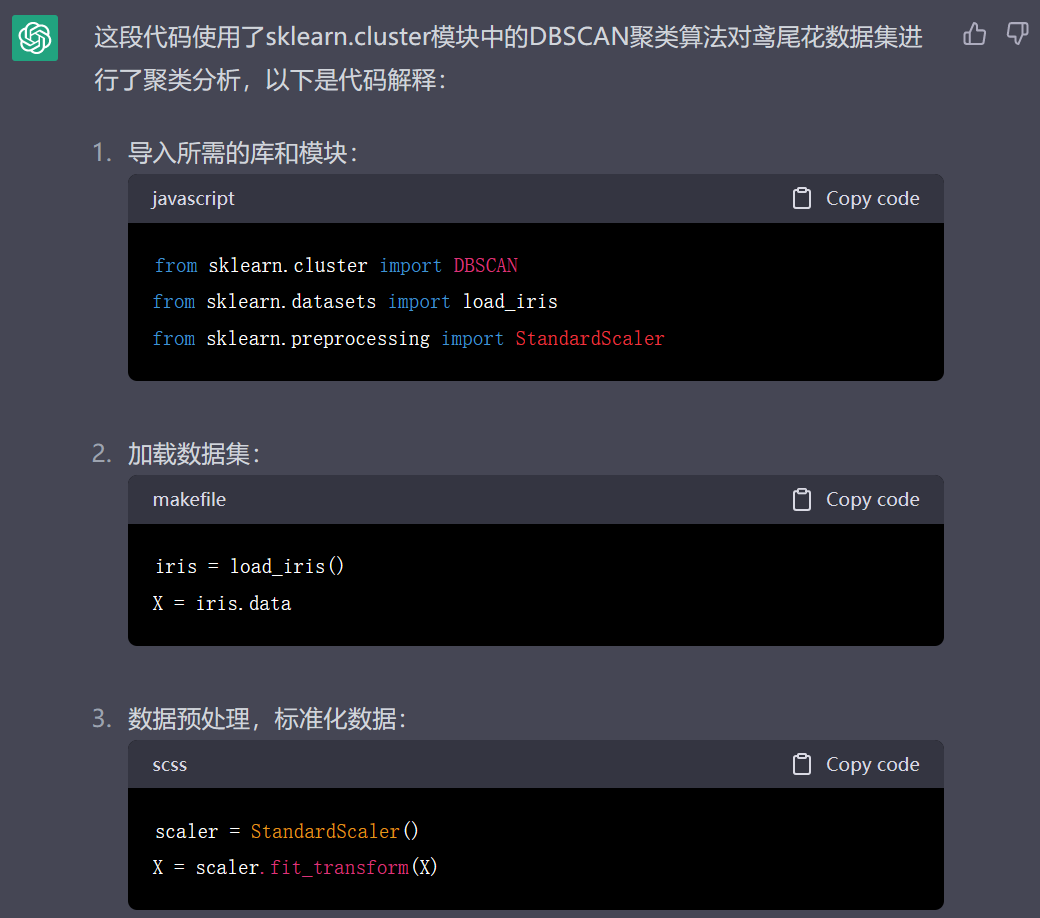
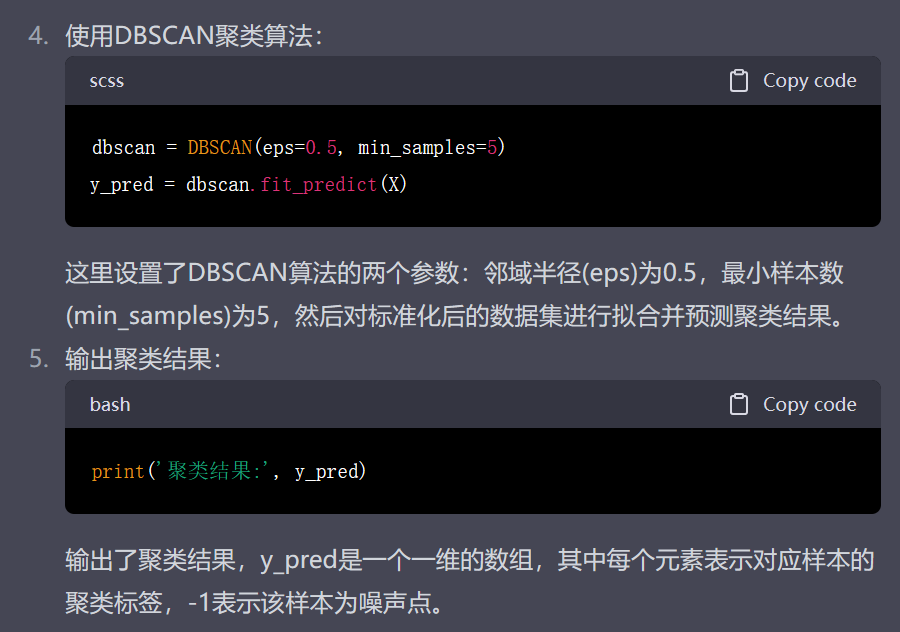
总之，这段代码演示了如何使用sklearn.cluster模块中的DBSCAN聚类算法对数据进行聚类分析，首先通过标准化对数据进行预处理，然后设置DBSCAN算法的参数，对数据集进行拟合和预测，最后输出聚类结果。

不过这次结果中将很多点设置为了噪声点（当然我们可以将噪声点归为一类），如果觉得现在的结果不满意，可以进一步调整算法中的参数。这里就省略了。

来源地址：https://blog.csdn.net/wzk4869/article/details/129775584