小编给大家分享一下LeetCode中广度优先搜索算法的示例分析,相信大部分人都还不怎么了解,因此分享这篇文章给大家参考一下,希望大家阅读完这篇文章后大有收获,下面让我们一起去了解一下吧!
一、认识广度优先搜索算法
广度优先搜索(BFS)算法是图的一种遍历方法,它的核心思想是从图的某一个节点开始,依次遍历相邻节点,再从这些相邻节点继续向外层节点遍历,直到连通图的所有节点均被访问到。
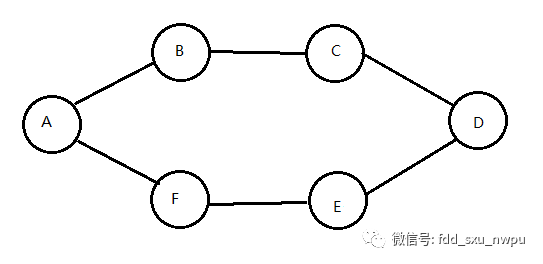
如上图所示,A、B、C、D、E、F六个节点构成了连通图。我们使用广度优先搜索算法对该连通图进行遍历,从A点出发,找到A点的相邻节点B点和F点,再分别找到B点和F点的相邻节点C点和E点,最终找到C点和E点的共同相邻节点D点。因此我们得到的遍历结果为ABFCED。
二、Leetcode常见广度优先搜索形式
当我们打开Leetcode的广度优先搜索标签,查看相关算法题时会发现,很多题是将连通图简化为树或二叉树的形式展示。因此我们可以从树/二叉树的角度分析广度优先搜索算法,只要搞懂了树的广度优先搜索,图的广度优先搜索只是相邻节点的选择差异罢了。
广度优先搜索算法在树/二叉树中被简化为层次遍历算法,即从树的根节点出发,依次遍历根节点的孩子,再分别将这些孩子作为根节点,循环上述操作,直至将所有的节点全部遍历结束。
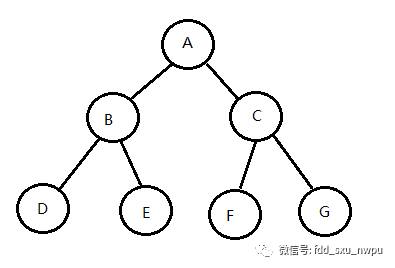
如下图所示,树的层次遍历就是一种特殊的广度优先搜索。根据上文的遍历规则不难得出树的广度优先搜索序列为ABCDEFG。
三、一道算法题讲解具体的BFS实现思路
我选取了Leetcode上一道典型的广度优先搜索算法给大家整理一下BFS的算法基本实现思路,题目如下:
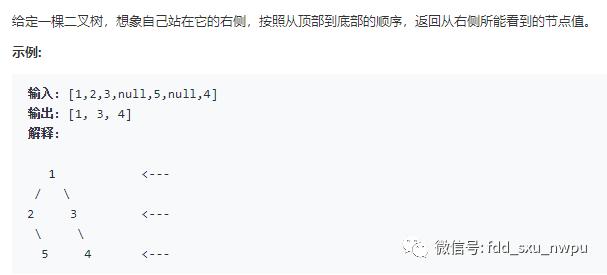
思路: 从题意中我们不难看出,该题的核心问题就是求出二叉树的每一层中最右边的节点的值并将其存入数组最后返回该数组。很显然,利用广度优先搜索算法可以很容易将每一层的最右节点求出。
对于广度优先搜索算法,我们需要申请一个辅助队列帮助我们存储每一层的每一个节点。首先需要对根节点判空,若根节点为空则直接返回一个空数组,否则将根节点存入队列中。接下来我们需要将队列中该层的所有节点取出,并找出它们的孩子节点存入队列中。需要注意的是,到了最右节点时应将该节点的值存入数组。循环该过程直至遍历二叉树的所有节点即可得出最终的结果。
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> ans = new ArrayList<>();
if (root == null) {
return ans;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
int count = queue.size();
TreeNode currentNode = null;
while (count > 0) {
count--;
currentNode = queue.poll();
if (currentNode.left != null) {
queue.add(currentNode.left);
}
if (currentNode.right != null) {
queue.add(currentNode.right);
}
}
ans.add(currentNode.val);
}
return ans;
}
}
算法复杂度分析:算法需要访问该二叉树中的每个节点并且每个节点的访问时间为O(1),所以最终的事件复杂度为O(n)。对于空间复杂度,我们申请了一个辅助队列帮助存储二叉树节点,最终的空间复杂度也可表示为O(n)。
以上是“LeetCode中广度优先搜索算法的示例分析”这篇文章的所有内容,感谢各位的阅读!相信大家都有了一定的了解,希望分享的内容对大家有所帮助,如果还想学习更多知识,欢迎关注编程网行业资讯频道!




