请点击↑关注、收藏，本博客免费为你获取精彩知识分享！有惊喜哟！！ 

一、单项选择题(共15题，每题2分，共计30分；每题有且仅有一个正确选项)

以下关于CSP-J/S的描述错误的是（）

A.参加CSP-S/J两组两轮认证均须在网上注册报名。未注册者，无认证成绩

B.CSP-J/S是中国计算机学会举办的程序设计竞赛

C.CSP-JS第二轮实行网上注册、报名，未通过网上报名的认证者可向所在省份特派员申请获得第二轮参加认证的资格

D.CSP-J/S认证成绩优异者，可参加NOI省级选拔，省级选拔成绩优异者可参加NOI

在8位二进制补码中，10110110表示的是十进制下的()  

A.202      B.74      C.-202      D.-74

2019年10月14日是星期一，1978年10月14日是()

A.星期日         B.星期五         C.星期一      D.星期六

图G是一棵n节点的树，G上有（）条边

A.n            B.2*n            C.n-1         D.n+1

由五个不同的节点构成的树有（）种

A. 3125    B. 125   C.32   D.1024

有一个长为6的A序列：{3,20,4,6,1}，现通过进行交换其中相邻两个数字的操作进行排序，要将A序列排成从小到大的递增序列最少要进行多少次交换操作（）

A.5        B.6            C.7            D.15

某算法计算时间表示为递推关系式：  T(N)=N+T(N/2) ,则该算法时间复杂度为( )。

A.O(N*N)      B.O(NlogN)      C.O(N)      D.O(1)

一棵6节点二叉树的中序遍历为DBAGECF,先序遍历为ABDCEGF，后序遍历为（）

A.  DGBEFAC                     B.  GBEACFD                     C.  DBGEFCA              D. ABCDEFG

一张有9个节点的无向图最多有()条边

A.40         B.81         C.72      D.36

下列不属于面向对象程序设计语言的是( )

A.C++         B. C         C.JAVA      D.C#

G是一张有n个点m条边的连通图，必须删去（）条边才能将其变成一棵n节点的树

A.1         B.m-n-1      C.m+n-1      D.m-n+1

字符串”abcab”本质不同的子串个数（）,不考虑空串

A.15     B.14      C.13       D.12

十进制小数13.375对应的二进制数是()：  

A.1101.011    B.1011.011    C.1101.101   D.1010.01

若某算法的计算时间表示为递推关系：

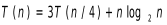
则该算法的复杂度为()

 一家三口人，恰好仅有两个人生日在同一天的概率是（）   【假设每年都是365天】

A．1/365         B.365/（364*365）               C.（3*364）/（365*365）            D.1/12

二、阅读程序写结果(共8小题，每小题5分，共计40分)

第一题

#include

using namespace std;

int a,b,c;

int main()

{

   cin>>a>>b>>c;

   int t=b;

   b=a,a=t;

   c=a;

   cout<

}

 若输入3 9 1，则输出9 3 3

A.正确

B.错误

 若输入12300400000 3 7，将一定能输出3 12300400000 3

A.正确

B.错误

该程序中，头文件#include可以改成#include

A.正确

B.错误

若输入3 6 9，输出()

A. 6 3 6

B. 9 3 3

C. 6 9 3

D. 6 3 3

若将c=a改成c=t,则若输入3 6 9，输出()

A. 6 3 6

B. 9 3 3

C. 6 9 3

D. 6 3 3

若将c=a改成c=b,则若输入3 6 9，输出()

A. 6 3 6

B. 6 3 9

C. 6 3 3

D. 3 6 3

第二题

#include

#include

#include

using namespace std;

int w[35000],d[35000],dp[35000];

int main()

{

    int n,m;

    scanf("%d%d",&n,&m);

    for(int i=1;i<=n;i++)< span="">

       scanf("%d%d",&w[i],&d[i]);

    for(int i=1;i<=n;i++)< span="">

    {

        for(int j=m;j>=w[i];j--)

        {

            dp[j]=max(dp[j],dp[j-w[i]]+d[i]);

        }

    }

    printf("%d\n",dp[m]);

    return 0;

}

上述代码中，双重循环里循环变量j的枚举顺序改为从w[i]到m，输出结果一定不变

A.正确

B.错误

上述代码中，双重循环中变量i的枚举顺序改为从n到1，输出结果一定不变

A.正确

B.错误

 当输入为：

   4 6

   1 4

   2 6

   3 12

   2 7

输出为()

A.17

B.28

C.29

D.23

若输入数据中，1<=n<=30000,1<=m<=30000,1<=w[i]<=30000,1<=d[i]<=30000,则所求答案一定没有溢出()< span="">

A.正确

B.错误

若输入数据中，1<=n<=30000,1<=m<=30000,1<=w[i]<=30000,1<=d[i]<=1000000000,则所求答案一定没有溢出()< span="">

A.正确

B.错误

上述代码的时间复杂度为()

A.O(n)

B.O(n*n*m)

C.O(n*m)

D.O(n*m*m)

第三题

#include

#include

#include

#define N 500+10

using namespace std;

int a[N],n;

int main()

{

 cin>>n;

 for(int i=1;i<=n;i++)cin>>a[i];

 for(int i=1;i

 {

 int tmp=i;

 for(int j=i+1;j<=n;j++)< span="">

 if(a[j]

 swap(a[i],a[tmp]);

 }

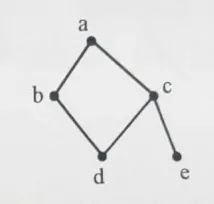
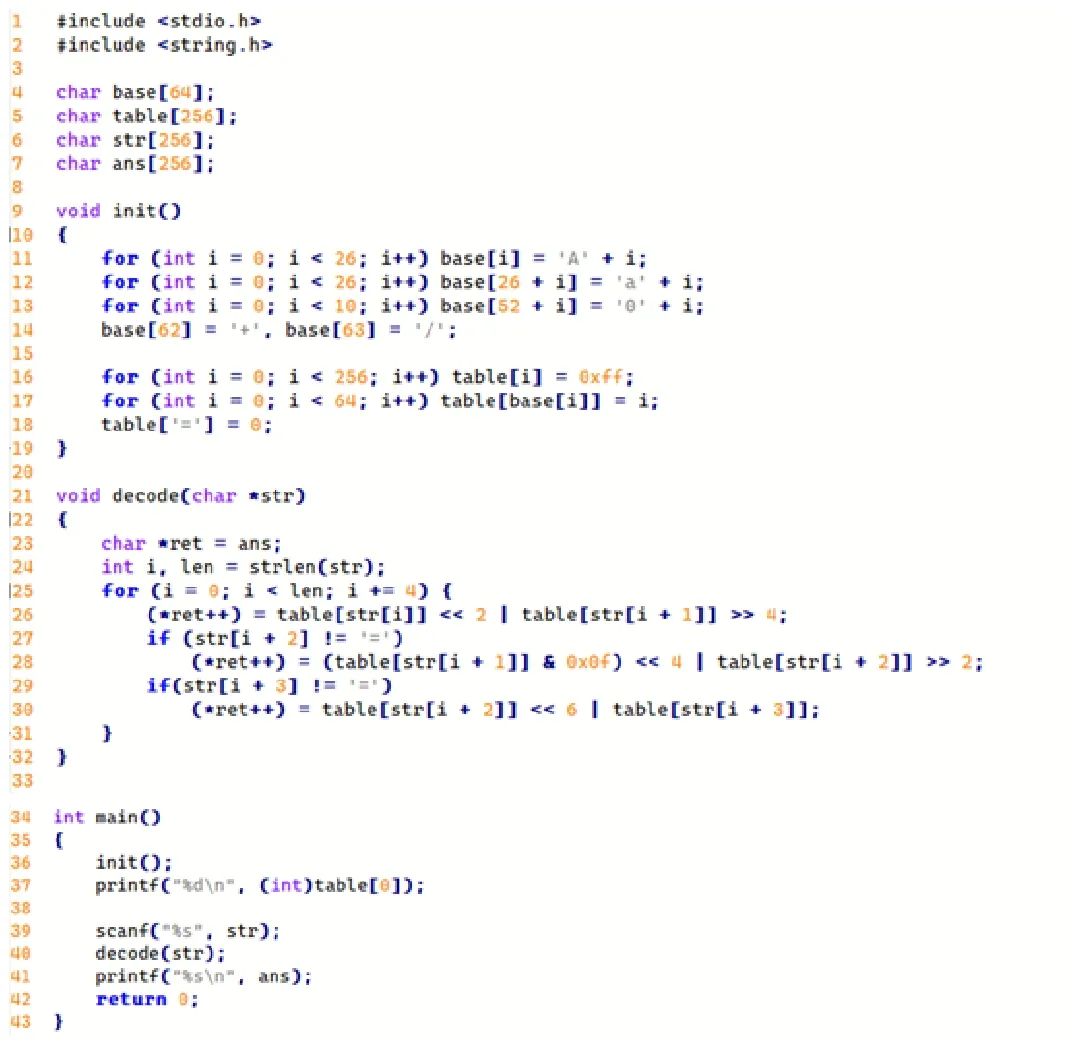
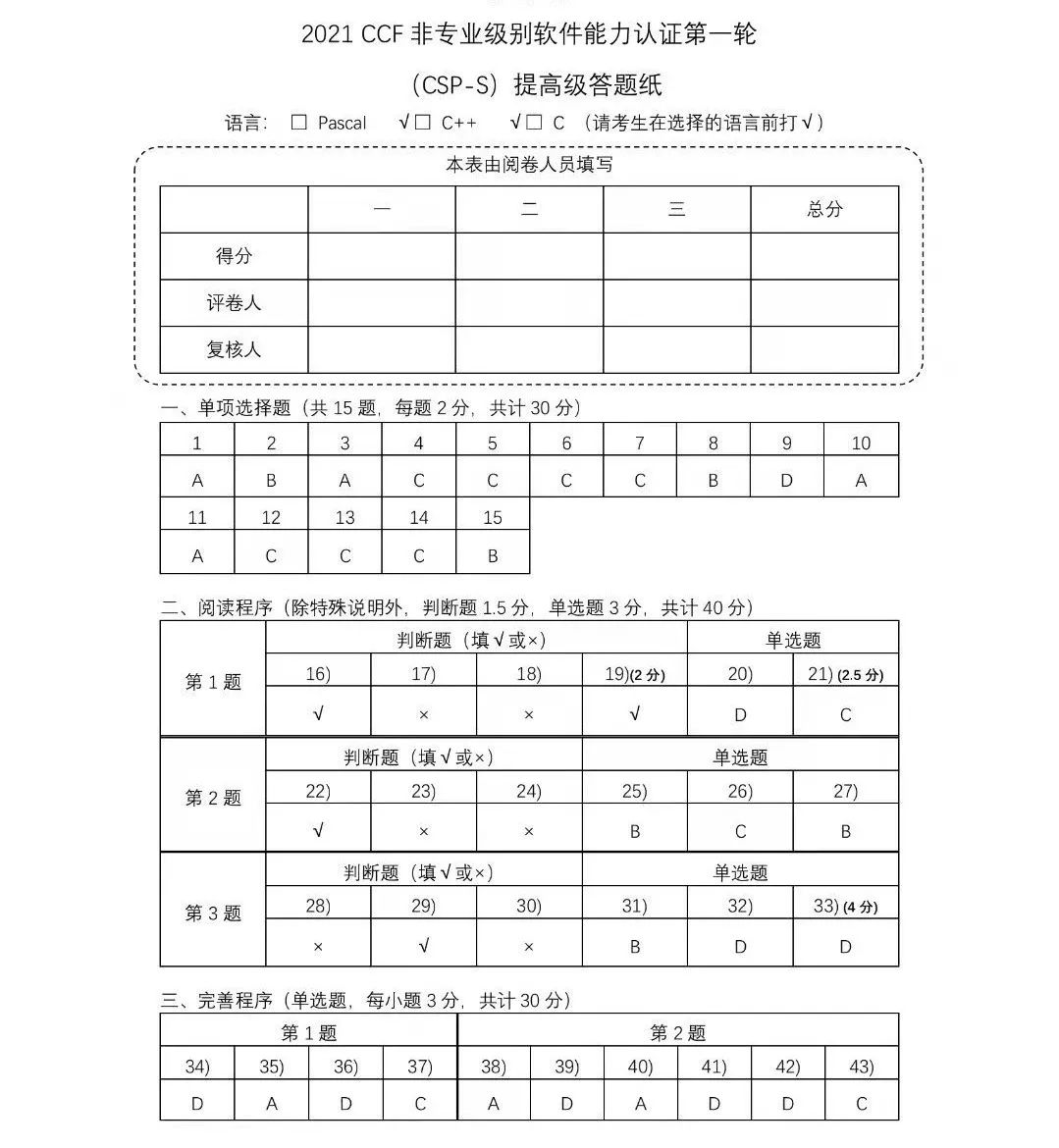
 for(int i=1;i<=n;i++)cout<

 cout<

 return 0;

}

上述代码实现了对一个长度为n的序列进行排序（）

A.正确

B.错误

我们将上述算法称为（）

A. KMP

B. 冒泡排序

C. 选择排序

D. 归并排序

上述代码的时间复杂度为()

A. O(n)  B. O(nlogn)  C. O(n*n)   D. O(n*n*n)

若输入数据为：

5

3 2 1 5 4

则if(a[j]

A. 5    B. 7    C.3   D.4

去掉头文件#include后程序仍能正常编译运行()

A.正确

B.错误

去掉using namespace std;后程序仍能正常编译运行()

A.正确

B.错误

五、完善程序(每题15分，共计30分)

 请完善下面的程序，使用BFS统计一张边权都为1的图中，从给定起点到所有点的距离：

#include

#include

#include

#define N 200020

using namespace std;

int n,m;

vectorG[N];

int q[N],hd,tl;

int dis[N];

void BFS(___（1）_____)

{

   hd=1,tl=0;

   for(int i=1;i<=n;i++)dis[i]=-1;< span="">

   q[++tl]=st,dis[st]=0;

   while(____(2)_____)

   {

      int u=q[hd++];

      for(int i=0;i

      {

         int v=G[u][i];

         if(____(3)____)continue;

         dis[v]=dis[u]+1;

         q[++tl]=v;

      }

   }

}

int main()

{

   scanf("%d%d",&n,&m);

   for(int i=1;i<=m;i++)< span="">

   {

      int x,y;

      scanf("%d%d",&x,&y);

      G[x].push_back(y);

      ______(4)________;

   }

   int st;

   scanf("%d",&st);

   BFS(st);

   for(_____(5)_____)printf("%d ",dis[i]);

}

上述程序___(1)___中应该填写（）

A.int u;

B.int st;

C.int &st;

D.int st

上述程序___(2)___中应该填写（）

A.hd

B.hd>tl

C.hd<=tl< span="">

D.hd>=tl

上述程序___(3)___中应该填写（）

A.vis[v]==true

B.dis[v]<=dis[u]< span="">

C.dis[v]!=-1

D.dis[v]>dis[u]

 上述程序___(4)___中应该填写（）

A.G[y].push_back(x)

B.G[y].insert(x)

C.G[y][x]=1

D.G[y].push(x)

 上述程序___5___中应该填写（）

A. int j=1;j<=n;j++< span="">

B. int i=1;i<=n;i++< span="">

C. int i=0;i

D. int i=1,i<=n,i++< span="">

(拓扑排序)给出一张n节点m条边的有向图，求出该图的一个拓扑排序，若无拓扑排序输出-1

输入：

第一行两个正整数 n,m 表示点数和边数。
接下来 m 行，每行三个正整数 x,y表示节点 x->y之间有一条边。

输出：

一个拓扑序：按拓扑序输出点的编号。若拓扑序不唯一，输出任意一个均可。若无拓扑序，输出 -1.

#include

#include

#include

#define N 200020

using namespace std;

int n,m;

vectorG[N];

int q[N],hd,tl;

int du[N];

int ans[N],tot;

void topo()

{

   hd=1,tl=0;

   for(int i=1;i<=n;i++)if(___(1)____)q[++tl]=i;< span="">

   while(hd<=tl)< span="">

   {

      int u=q[hd++];

      ans[++tot]=u;

      for(int i=0;____(2)____;i++)

      {

         int v=G[u][i];

         du[v]--;

         if(!du[v])____(3)____;

      }

   }

   if(tot!=n)puts("-1");

   else

   {

      for(int i=1;i<=n;i++)< span="">

         printf("%d ",ans[i]);

   }

}

int main()

{

   scanf("%d%d",&n,&m);

   for(int i=1;i<=m;i++)< span="">

   {

      int x,y;

      scanf("%d%d",&x,&y);

      _____(4)___________;

      _____(5)___________;

   }

   topo();

}

 上述程序___1___中应该填写（）

A. du[i]

B. q[i]

C. hd<=tl< span="">

D. !du[i]

 上述程序___2___中应该填写（）

A. i<=n< span="">

B. i

C. i

D. i<=g[u].size()< span="">

 上述程序___3___中应该填写（）

A. q[++tl]=v

B. q[tl++]=v

C. q[++hd]=v

D. q[hd++]=v

 上述程序___4___中应该填写（）

A.G[y].push_back(x)

B.G[x].push_back(y)

C.G[x].push(y)

D.G[y].push(x)

 上述程序___5___中应该填写（）

A.G[y].push_back(x)

B.G[y].push(x)

C.du[y]++

D.du[x]++

CSP-S模拟卷参考答案

 2021年CSP-S提高级第一轮试题

一、单项选择题（共15题，每题2分，共计30分：每题有且仅有一个正确选项）

 以下不属于面向对象程序设计语言的是（D）。

A. C++

B. Python

C. Java

D. C

 以下奖顼与计算机领域最相关的是（B）。

A. 奧斯卡奖

B. 图灵奖

C. 诺贝尔奖

D. 普利策奖

 目前主流的计算机储存数据最终都是转换成（A）数据进行存储。

A. 二进制

B. 十进制

C. 八进制

D. 十六进制

 以比较作为基本运算，在N个数中找出最大数，最坏情况下所需要的最少的比较次数为（C）。

A. N^2

B. N

C. N-1

D. N+1

  对于入栈顺序为a,b,c,d,e的序列，下列（D）不是合法的出栈序列。

A. a,b,c,d,e

B. e,d,c,b,a

C. b,a,c,d,e

D. c,d,a,e,b

 对于有n个顶点、m条边的无向联通图（m>n）,需要删掉（D）条边才能使其成为一棵树。

A. n-1

B. m-n

C. m-n-1

D. m-n+1

 二进制数101.11对应的十进制数是（C）。

A. 6.5

B. 5.5

C. 5.75

D. 5.25

 如果一棵二叉树只有根结点，那么这棵二叉树高度为1。请问高度为5的完全二叉树有（A）种不同形态？

A. 16

B. 15

C. 17

D. 32

 表达式a*(b+c)*d的后缀表达式为（B），,其中”*”和”+”是运算符。

A. **a+bcd

B. abc+*d*

C. abc+d**

D. *a*+bcd

6个人，两个人组一队，总共组成三只，不区分队伍的编号，不同的组队情况有（B）种。

A. 10

B. 15

C. 30

D. 20

 在数据压缩编码中的哈夫曼编码方法，在本质是一种（B）的策略。

A. 枚举

B. 贪心

C. 递归

D. 动态规划

 由1, 1, 2, 2, 3这五个数字组成不同的三位数有（A）种。

A. 18

B. 15

C. 12

D. 24

 考虑如下递归算法

solve(n)

if n<=1 return 1

else if n>=5 return n*solve(n-2)

else return n*solve(n-1)

则调用solve(7)得到的返回结果为（C）。

A. 105

B. 840

C. 210

D. 420

 以a为起点，对右边的无向图进行深度优先遍历，则b、c、d、e四个点中有可能作为最后一个遍历到的点个数为（B）。

A. 1

B. 2

C. 3

D. 4

 有四个人要从A点做一条船过河到B点，船一开始在A点。该船一次最多可坐两个人。已知这四个人中每个人独自坐船的过河时间分别为1, 2, 4, 8, 且两个人坐船的过河时间为两人独自过河时间的较大者。则最短（B）时间可以让四个人都过河到B点（包括从B点把船开回A点时间）。

A. 14

B. 15

C. 16

D. 17 

二、阅读程序（程序输入不超过数组或字符串定义的范围；判断题正确填 √，错误填X；除特殊说明外，判断题1.5分，选择题3分，共计40分）

(1)

判断题

 输入的n等于1001时，程序不会发生下标越界。（X）

 输入的a[i]必须全为正整数，否则程序将陷入死循环。（X）

 当输入”5 2 11 9 16 10”时，输出为”3 4 3 17 5” 。（X）

 当输入为”1 511998“时，输出为”18” 。（√）

 将源代码中g函数的定义（13-16行）移到main函数的后面，程序可以正常编译运行。（X）

单选题

 当输入为”2 -65536 2147483647”时，输出为（B）。

A. "65532 33”

B. "65552 32"

C. "65535 34"

D. "65554 33" 

(2)

判断题

 输出的第二行一定是由小写字母、大写字母、数字和“+”、“/”、“=”构成的字符串。（X）

 可能存在输入不同，但输出的第二行相同的情形。（√）

 输出的第一行为“-1”。（ √）

单选题

 设输入字符串长度为n，decode函数的时间复杂度为（B）。

A. θ(√n)

B. θ(n)

C. θ(nlogn)

D. θ(n^2)

 当输入为“Y3Nx”时，输出的第二行为（B）。

A. “csp”

B. “csq”

C. “CSP”

D. “Csp”

 （3.5分）当输入为“Y2NmIDIwMjE=”时，输出的第二行为（C）。

A. “ccf2021”

B. “ccf2022”

C. “ccf 2021”

D. “ccf 2022” 

(3)

假设输入的x是不超过1000的自然数，完成下面的判断题和单选题：

判断题

 若输入不为"1"，把第12行删去不会影响输出的结果。（√）

 （2分）第24行的" f[i]/c[i*k]"可能存在无法整除而向下取整的情况。（X）

 （2分）在执行完init()后，f数组不是单调递增的，但g数组是单调递增的。（X）

单选题

init函数的时间复杂度为（A）。

A. θ(n)

B. θ(nlogn)

C. θ(n√n)

D. θ(n^2)

 在执行完init()后，f[1], f[2], f[3] ...... f[100]中有（C）个等于2。

A. 23

B. 24

C. 25

D. 26

 （4分）当输入"1000"时，输出为（C）。

A. "15 1340"

B. "15 2340"

C. "16 2340"

D. "16 1340"

三、完善程序（单选题，每小题3分，共计30分）

 (1)（Josephus 问题）有 n 个人围城一个圈，依次标号 0 至 n-1。从 0 号开始，依次 0, 1, 0, 1, ... 交替报数，报到 1 的人会离开，直至圈中只剩下一个人。求最后剩下人的编号。

试补全模拟程序。

①处应填（D）

A. i < n

B. c < n

C. i < n - 1

D. c < n - 1

②处应填（C）

A. i % 2 == 0

B. i % 2 == 1

C. p

D. !p

③处应填（C）

A. i++

B. i = (i + 1) % n

C. c++

D. p ^= 1

④处应填（D）

A. i++

B. i = (i + 1) % n

C. c++

D. p ^= 1

⑤处应填（B）

A. i++

B. i = (i + 1) % n

C. c++

D. p ^= 1 

(2)（矩形计数）平面上有n个关键点，求有多少个四条边都和x轴或者y轴平行的矩形，满足四个顶点都是关键点。给出的关键点可能有重复，但完全重合的矩形只计一次。

试补全枚举算法。

①处应填（B）

A. a.x != b.x ? a.x < b.x : a.id < b.id

B. a.x != b.x ? a.x < b.x : a.y < b.y

C. equals(a,b) ? a.id < b.id : a.x < b.x

D. equals(a,b) ? a.id < b.id : (a.x != b.x ? a.x < b.x : a.y < b.y)

②处应填（D）

A. i == 0 || cmp(A[i], A[i - 1])

B. t == 0 || equals(A[i], A[t - 1])

C. i == 0 || !cmp(A[i], A[i - 1])

D. t == 0 || !equals(A[i], A[t - 1])

③处应填（C）

A. b - (b - a) / 2 + 1

B. (a + b + 1) >> 1

C. (a + b) >> 1

D. a + (b - a + 1) / 2

④处应填（B）

A. !cmp(A[mid], p)

B. cmp(A[mid], p)

C. cmp(p, A[mid])

D. !cmp(p, A[mid])

⑤处应填（D）

A. A[i].x == A[j].x

B. A[i].id < A[j].id

C. A[i].x == A[j].x && A[i].id < A[j].id

D. A[i].x < A[j].x && A[i].y < A[j].y

2021年CSP-S提高级第一轮试题                                                                                                                                                                                                                    

来源地址：https://blog.csdn.net/weixin_68261415/article/details/129933876