最近在学习数据分析线性回归算法时,产生了很多疑问。作为初学者,我认为应该先从基本概念上进行一些深度理解。下面将我的一些思考总结如下:
线性回归模型为: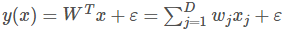 (1)
(1)
其中ε是剩余误差,假设它服从的是高斯分布,然后因此就将线性回归模型和高斯模型联合起来,获取公式如下:

到这里我是完全没看懂!
对于线性回归我有4个疑问:
第一:看到的诸多线性回归、逻辑回归什么的,回归到底是什么意思?
第二:这个ε剩余误差又有什么样的意义?
第三:为什么剩余误差服从高斯分布(即正态分布),整个线性回归模型就能写成高斯分布模型?
第四:这里的线性到底指的是什么?
接下来,我将针对这四个问题谈一谈自己的理解。
1. 回归指的是什么意思?
回归,即将现有的数据向假设的模型拟合接近,还原真实的数据模式。
2. 如何理解ε剩余误差?
这里不妨把(1)式进行合适的转换: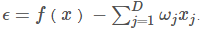 (2)
(2)
这样就更容易理解,也就是我们只简单地用线性模型来拟合真是的变量间的关系,并不能达到完美的解释。所以,ε就弥补了用模型难以解释的那一部分,即模型外的未知因素的影响。
3. 为什么剩余误差符合高斯分布,整个线性模型就符合高斯分布?
看公式(2)应该可以较容易理解,这是纯粹的数学知识。
4. 这里的线性到底指的是什么?
关于线性模型中的线性有三种说法:
(1)变量和参数都是线性的;
(2)变量是线性的,但参数不是线性的;
(3)参数是线性的,但变量不是线性的。
而我们这里所说的线性模型主要是针对(3)而言的。所以只要参数是线性的这类问题,我们对变量无论是转成指数、幂指数等任意一种函数形式,都可以用线性模型来解决问题,因为我们要学习的是这个参数向量,而变量值是确定的。




