什么是平衡二叉树AVL,很多新手对此不是很清楚,为了帮助大家解决这个难题,下面小编将为大家详细讲解,有这方面需求的人可以来学习下,希望你能有所收获。
前言
Wiki:在计算机科学中,AVL树是最早被发明的自平衡二叉查找树。在AVL树中,任一节点对应的两棵子树的最大高度差为1,因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是 O(logn)。增加和删除元素的操作则可能需要借由一次或多次树旋转,以实现树的重新平衡。AVL 树得名于它的发明者 G. M. Adelson-Velsky 和 Evgenii Landis,他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。
1 为什么要有平衡二叉树
二叉搜索树一定程度上可以提高搜索效率,但是当原序列有序时,例如序列 A = {1,2,3,4,5,6},构造二叉搜索树如图 1.1。依据此序列构造的二叉搜索树为右斜树,同时二叉树退化成单链表,搜索效率降低为 O(n)。
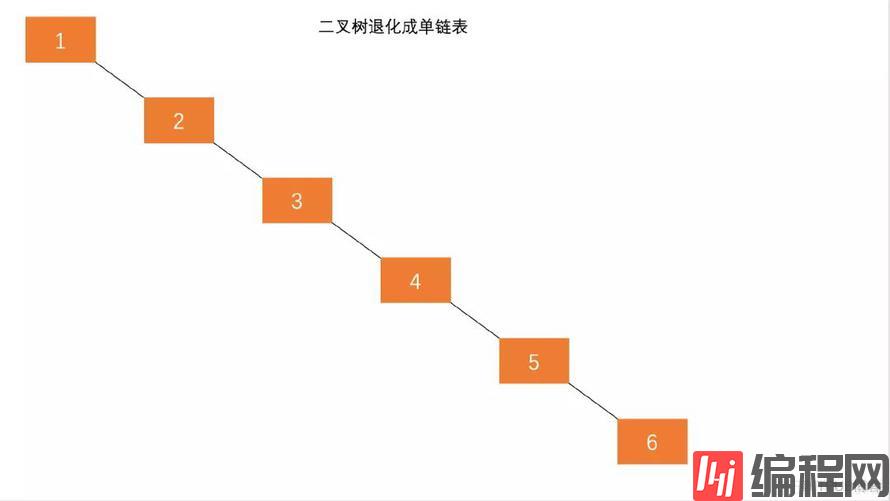
在此二叉搜索树中查找元素 6 需要查找 6 次。
二叉搜索树的查找效率取决于树的高度,因此保持树的高度最小,即可保证树的查找效率。同样的序列 A,将其改为图 1.2 的方式存储,查找元素 6 时只需比较 3 次,查找效率提升一倍。
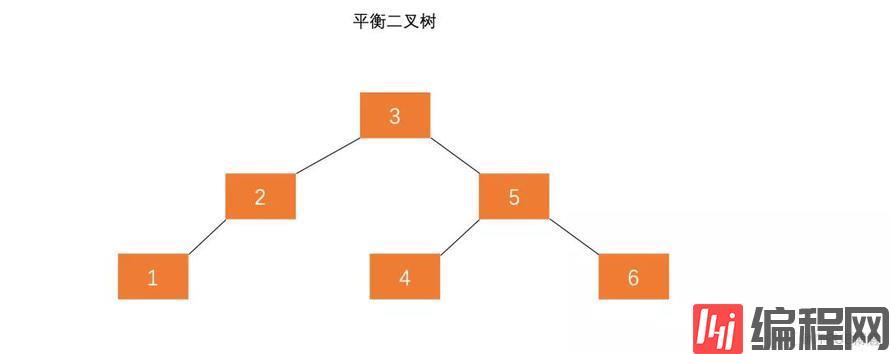
可以看出当节点数目一定,保持树的左右两端保持平衡,树的查找效率最高。
这种左右子树的高度相差不超过 1 的树为平衡二叉树。
2. 定义
平衡二叉查找树:简称平衡二叉树。由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962 年提出的高度平衡的二叉树,根据科学家的英文名也称为 AVL 树。它具有如下几个性质:
可以是空树。
假如不是空树,任何一个节点的左子树与右子树都是平衡二叉树,并且高度之差的绝对值不超过 1。
平衡之意,如天平,即两边的分量大约相同。
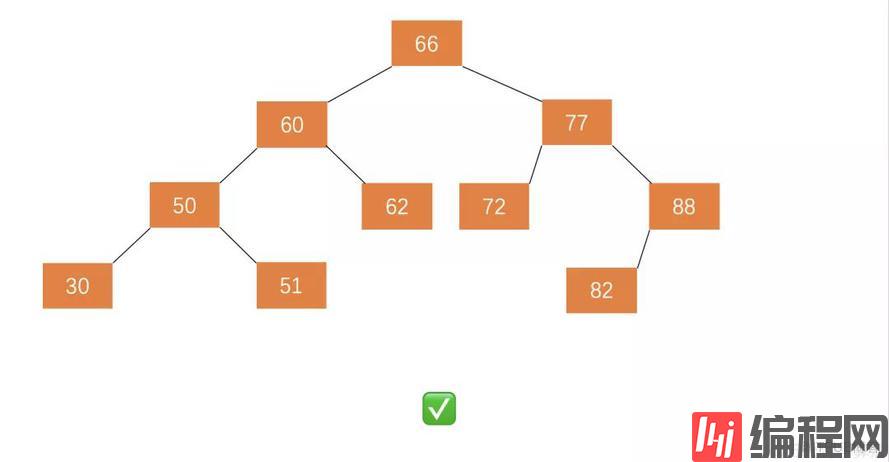
例如图 2.1 不是平衡二叉树,因为节点 60 的左子树不是平衡二叉树。
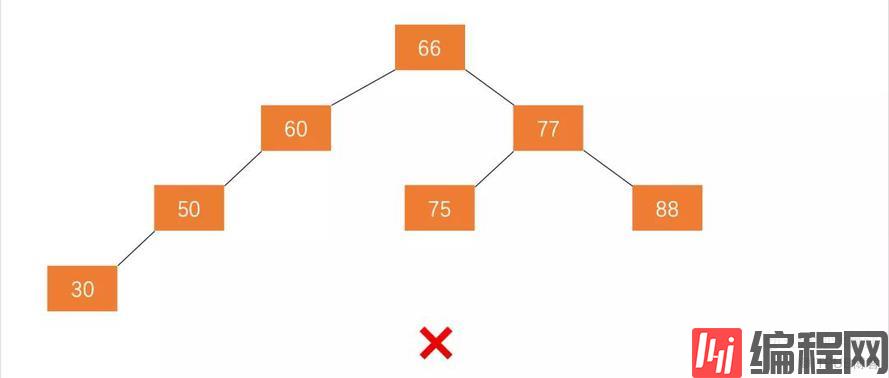
图 2.2 也不是平衡二叉树,因为虽然任何一个节点的左子树与右子树都是平衡二叉树,但高度之差已经超过 1 。
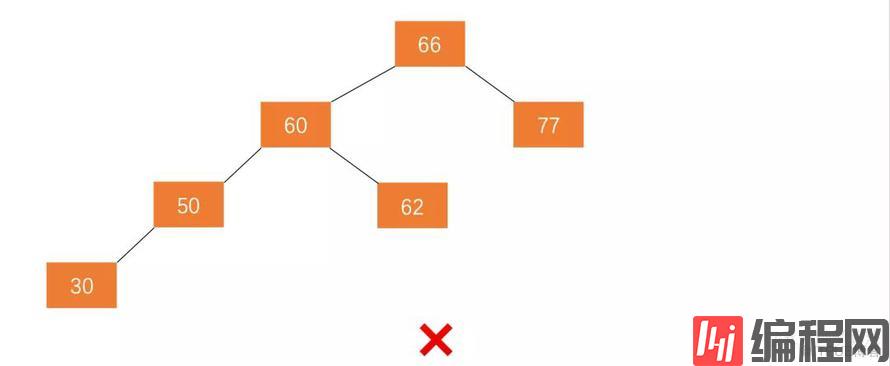
图 2.3 是平衡二叉树。
3. 平衡因子
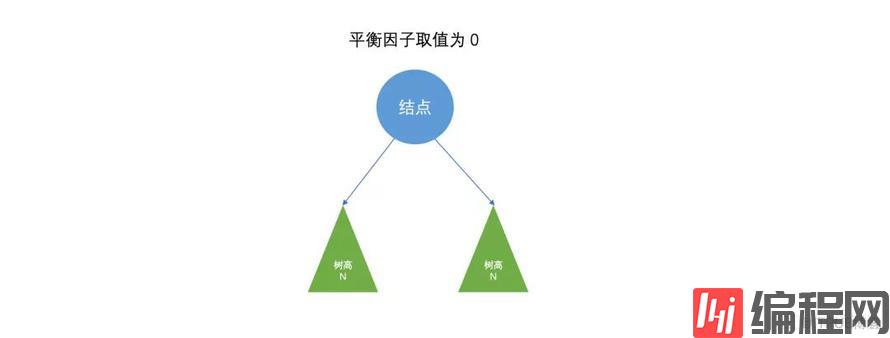
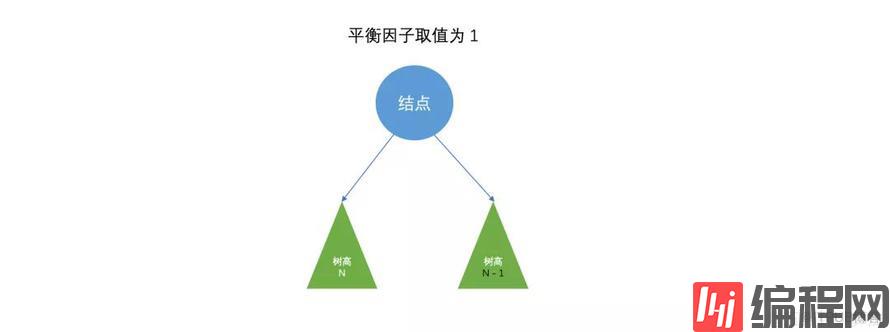
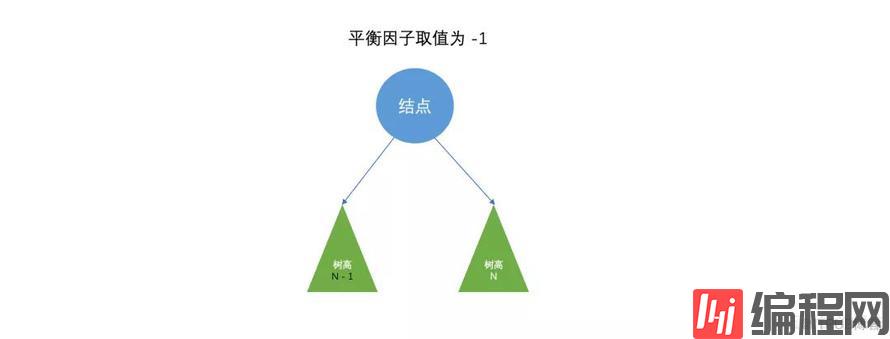
定义:某节点的左子树与右子树的高度(深度)差即为该节点的平衡因子(BF,Balance Factor),平衡二叉树中不存在平衡因子大于 1 的节点。在一棵平衡二叉树中,节点的平衡因子只能取 0 、1 或者 -1 ,分别对应着左右子树等高,左子树比较高,右子树比较高。
4. 节点结构
定义平衡二叉树的节点结构:
typedef struct AVLNode *Tree;
typedef int ElementType;
struct AVLNode{
int depth; //深度,这里计算每个节点的深度,通过深度的比较可得出是否平衡
Tree parent; //该节点的父节点
ElementType val; //节点值
Tree lchild;
Tree rchild;
AVLNode(int val=0) {
parent = NULL;
depth = 0;
lchild = rchild = NULL;
this->val=val;
}
};
5. AVL树插入时的失衡与调整
图 5.1 是一颗平衡二叉树
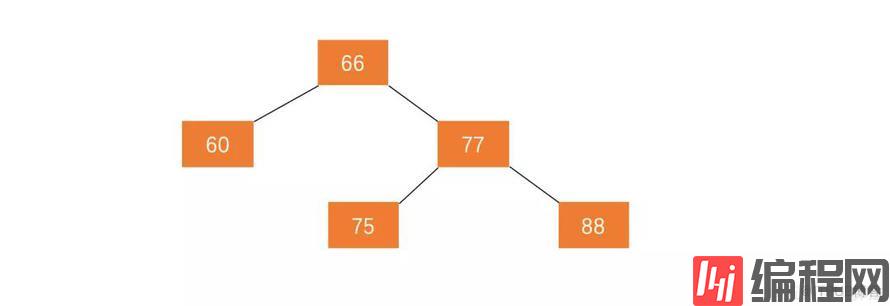
在此平衡二叉树插入节点 99 ,树结构变为:
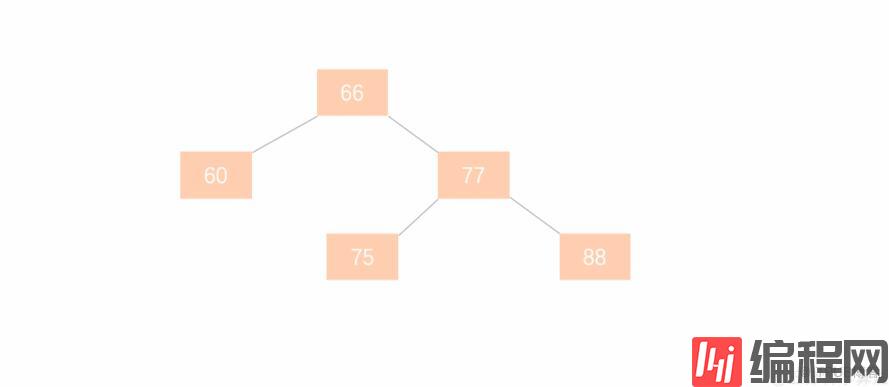
在动图 5.2 中,节点 66 的左子树高度为 1,右子树高度为 3,此时平衡因子为 -2,树失去平衡。
在动图 5.2 中,以节点 66 为父节点的那颗树就称为 最小失衡子树。
最小失衡子树:在新插入的节点向上查找,以第一个平衡因子的绝对值超过 1 的节点为根的子树称为最小不平衡子树。也就是说,一棵失衡的树,是有可能有多棵子树同时失衡的。而这个时候,我们只要调整最小的不平衡子树,就能够将不平衡的树调整为平衡的树。
平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。根据旋转的方向有两种处理方式,左旋 与 右旋 。
旋转的目的就是减少高度,通过降低整棵树的高度来平衡。哪边的树高,就把那边的树向上旋转。
5.1 左旋
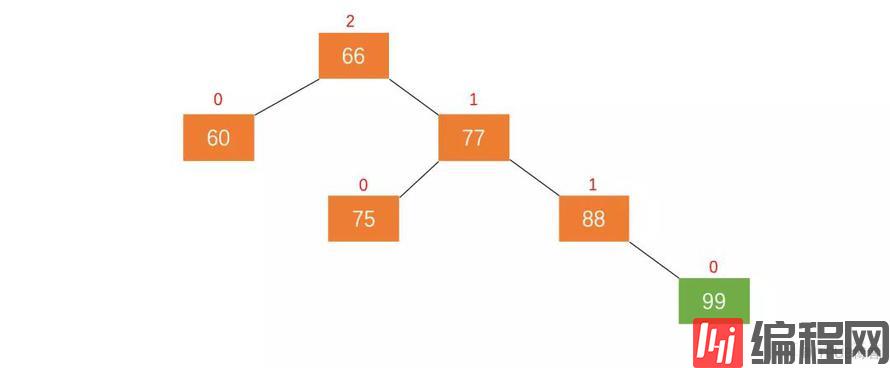
以图 5.1.1 为例,加入新节点 99 后, 节点 66 的左子树高度为 1,右子树高度为 3,此时平衡因子为 -2。为保证树的平衡,此时需要对节点 66 做出旋转,因为右子树高度高于左子树,对节点进行左旋操作,流程如下:
(1)节点的右孩子替代此节点位置
(2)右孩子的左子树变为该节点的右子树
(3)节点本身变为右孩子的左子树
整个操作流程如动图 5.1.2 所示。
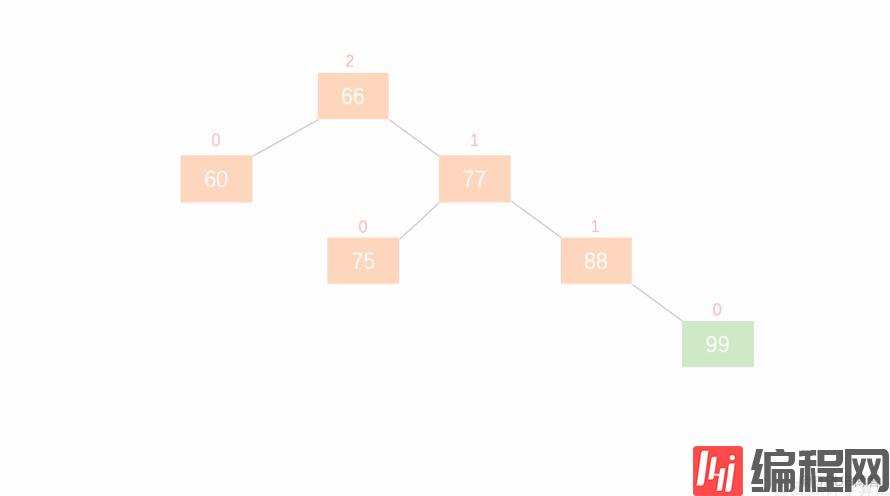
节点的右孩子替代此节点位置 —— 节点 66 的右孩子是节点 77 ,将节点 77 代替节点 66 的位置
右孩子的左子树变为该节点的右子树 —— 节点 77 的左子树为节点 75,将节点 75 挪到节点 66 的右子树位置
节点本身变为右孩子的左子树 —— 节点 66 变为了节点 77 的左子树
5.2 右旋
右旋操作与左旋类似,操作流程为:
(1)节点的左孩子代表此节点
(2)节点的左孩子的右子树变为节点的左子树
(3)将此节点作为左孩子节点的右子树。
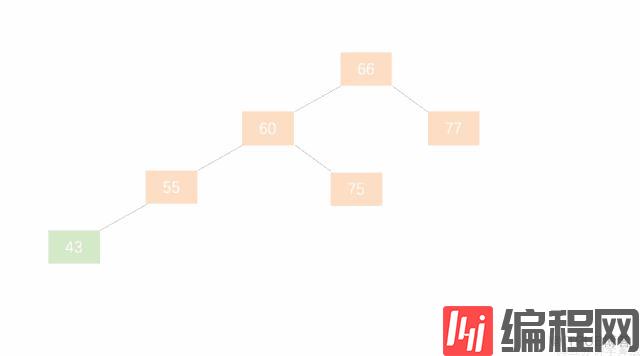
6. AVL树的四种插入节点方式
假设一颗 AVL 树的某个节点为 A,有四种操作会使 A 的左右子树高度差大于 1,从而破坏了原有 AVL 树的平衡性。平衡二叉树插入节点的情况分为以下四种:

具体分析如下:
6.1 A的左孩子的左子树插入节点(LL)
只需要执行一次右旋即可。

实现代码如下:
//LL型调整函数
//返回:新父节点
Tree LL_rotate(Tree node){
//node为离操作节点最近的失衡的节点
Tree parent=NULL,son;
//获取失衡节点的父节点
parent=node->parent;
//获取失衡节点的左孩子
son=node->lchild;
//设置son节点右孩子的父指针
if (son->rchild!=NULL) son->rchild->parent=node;
//失衡节点的左孩子变更为son的右孩子
node->lchild=son->rchild;
//更新失衡节点的高度信息
update_depth(node);
//失衡节点变成son的右孩子
son->rchild=node;
//设置son的父节点为原失衡节点的父节点
son->parent=parent;
//如果失衡节点不是根节点,则开始更新父节点
if (parent!=NULL){
//如果父节点的左孩子是失衡节点,指向现在更新后的新孩子son
if (parent->lchild==node){
parent->lchild=son;
}else{
//父节点的右孩子是失衡节点
parent->rchild=son;
}
}
//设置失衡节点的父亲
node->parent=son;
//更新son节点的高度信息
update_depth(son);
return son;
}
6.2 A的右孩子的右子树插入节点(RR)
只需要执行一次左旋即可。
实现代码如下:
//RR型调整函数
//返回新父节点
Tree RR_rotate(Tree node){
//node为离操作节点最近的失衡的节点
Tree parent=NULL,son;
//获取失衡节点的父节点
parent=node->parent;
//获取失衡节点的右孩子
son=node->rchild;
//设置son节点左孩子的父指针
if (son->lchild!=NULL){
son->lchild->parent=node;
}
//失衡节点的右孩子变更为son的左孩子
node->rchild=son->lchild;
//更新失衡节点的高度信息
update_depth(node);
//失衡节点变成son的左孩子
son->lchild=node;
//设置son的父节点为原失衡节点的父节点
son->parent=parent;
//如果失衡节点不是根节点,则开始更新父节点
if (parent!=NULL){
//如果父节点的左孩子是失衡节点,指向现在更新后的新孩子son
if (parent->lchild==node){
parent->lchild=son;
}else{
//父节点的右孩子是失衡节点
parent->rchild=son;
}
}
//设置失衡节点的父亲
node->parent=son;
//更新son节点的高度信息
update_depth(son);
return son;
}
6.3 A的左孩子的右子树插入节点(LR)
若 A 的左孩子节点 B 的右子树 E 插入节点 F ,导致节点 A 失衡,如图:
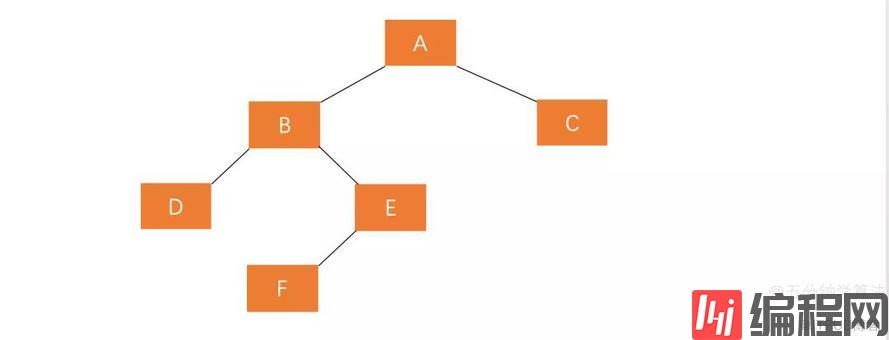
A 的平衡因子为 2 ,若仍按照右旋调整,则变化后的图形为这样:
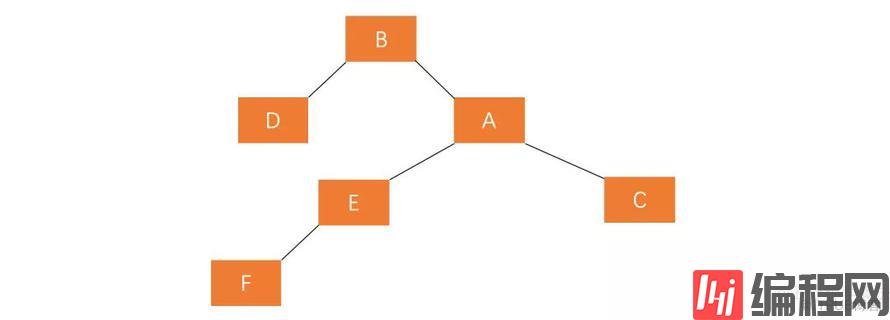
经过右旋调整发现,调整后树仍然失衡,说明这种情况单纯的进行右旋操作不能使树重新平衡。那么这种插入方式需要执行两步操作,使得旋转之后为 原来根节点的左孩子的右孩子作为新的根节点。
(1)对失衡节点 A 的左孩子 B 进行左旋操作,即上述 RR 情形操作。
(2)对失衡节点 A 做右旋操作,即上述 LL 情形操作。
调整过程如下:
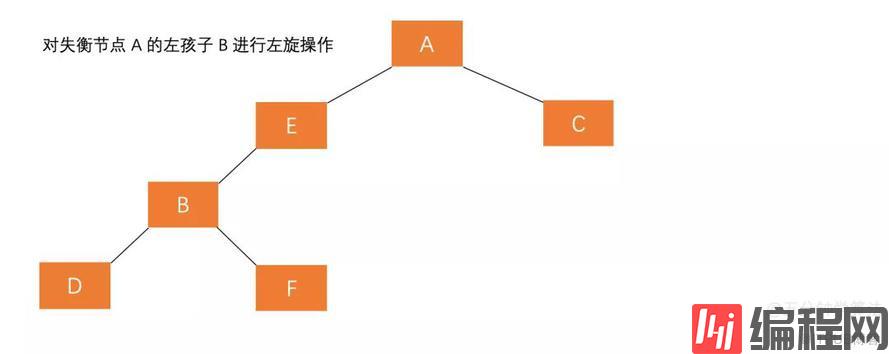
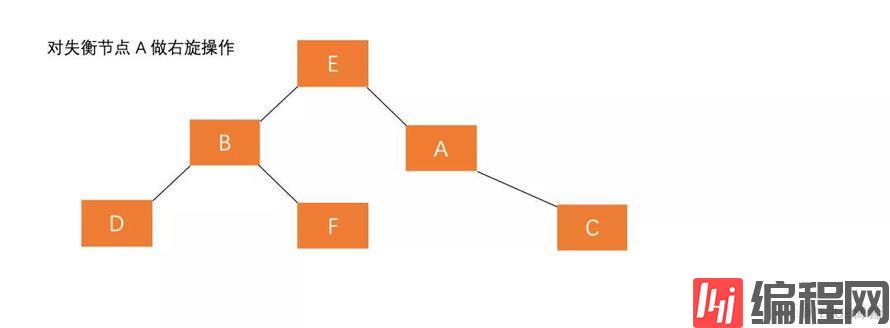
也就是说,经过这两步操作,使得 原来根节点的左孩子的右孩子 E 节点成为了新的根节点。
代码实现:
//LR型,先左旋转,再右旋转
//返回:新父节点
Tree LR_rotate(Tree node){
RR_rotate(node->lchild);
return LL_rotate(node);
}
6.4 A的右孩子的左子树插入节点(RL)
右孩子插入左节点的过程与左孩子插入右节点过程类似,也是需要执行两步操作,使得旋转之后为 原来根节点的右孩子的左孩子作为新的根节点。
(1)对失衡节点 A 的右孩子 C 进行右旋操作,即上述 LL 情形操作。
(2)对失衡节点 A 做左旋操作,即上述 RR 情形操作。
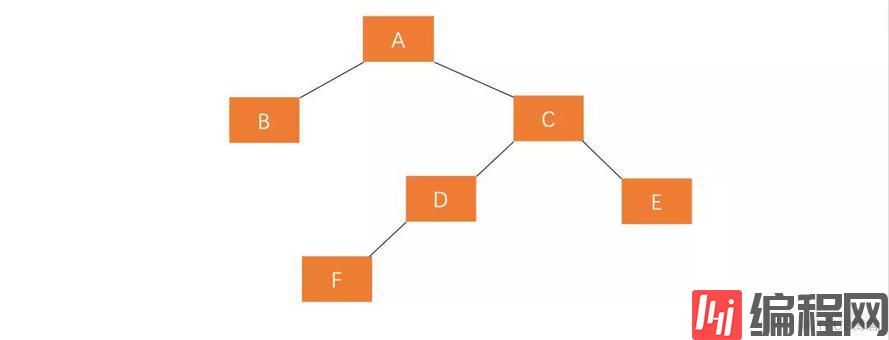
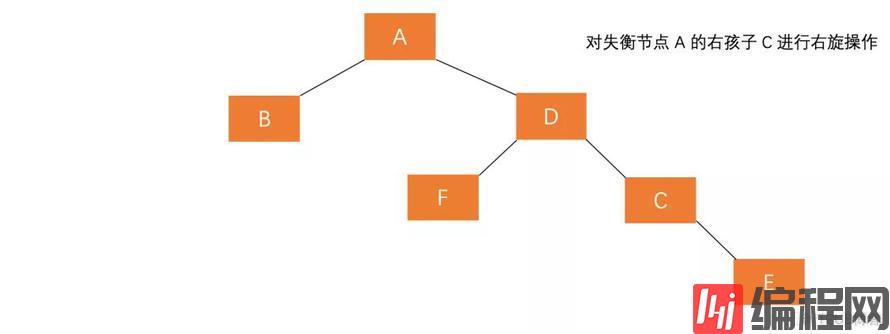
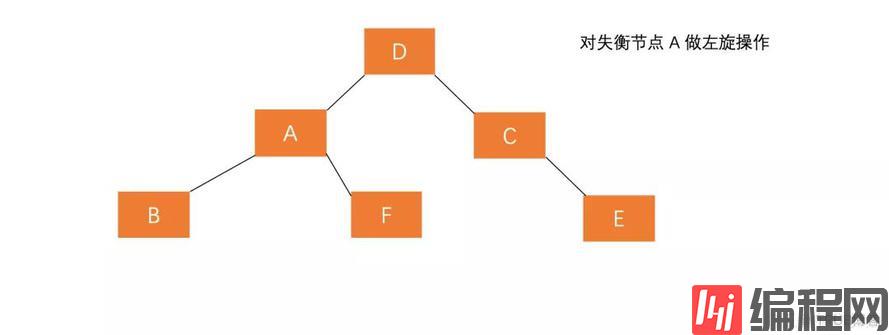
也就是说,经过这两步操作,使得 原来根节点的右孩子的左孩子 D 节点成为了新的根节点。
代码实现:
//RL型,先右旋转,再左旋转
//返回:新父节点
Tree RL_rotate(Tree node){
LL_rotate(node->rchild);
return RR_rotate(node);
}
补充:
上述四种插入方式的代码实现的辅助代码如下:
//更新当前深度
void update_depth(Tree node){
if (node==NULL){
return;
}else{
int depth_Lchild=get_balance(node->lchild); //左孩子深度
int depth_Rchild=get_balance(node->rchild); //右孩子深度
node->depth=max(depth_Lchild,depth_Rchild)+1;
}
}
//获取当前节点的深度
int get_balance(Tree node){
if (node==NULL){
return 0;
}
return node->depth;
}
//返回当前平衡因子
int is_balance(Tree node){
if (node==NULL){
return 0;
}else{
return get_balance(node->lchild)-get_balance(node->rchild);
}
}
6.5 小总结
在所有的不平衡情况中,都是按照先 寻找最小不平衡树,然后 寻找所属的不平衡类别,再 根据 4 种类别进行固定化程序的操作。
LL , LR ,RR ,RL其实已经为我们提供了最后哪个节点作为新的根指明了方向。如 LR 型最后的根节点为原来的根的左孩子的右孩子,RL 型最后的根节点为原来的根的右孩子的左孩子。只要记住这四种情况,可以很快地推导出所有的情况。
维护平衡二叉树,最麻烦的地方在于平衡因子的维护。建议读者们根据小吴提供的图片和动图,自己动手画一遍,这样可以更加感性的理解操作。
7. AVL树的四种删除节点方式
AVL 树和二叉查找树的删除操作情况一致,都分为四种情况:
(1)删除叶子节点
(2)删除的节点只有左子树
(3)删除的节点只有右子树
(4)删除的节点既有左子树又有右子树
只不过 AVL 树在删除节点后需要重新检查平衡性并修正,同时,删除操作与插入操作后的平衡修正区别在于,插入操作后只需要对插入栈中的弹出的第一个非平衡节点进行修正,而删除操作需要修正栈中的所有非平衡节点。
删除操作的大致步骤如下:
以前三种情况为基础尝试删除节点,并将访问节点入栈。
如果尝试删除成功,则依次检查栈顶节点的平衡状态,遇到非平衡节点,即进行旋转平衡,直到栈空。
如果尝试删除失败,证明是第四种情况。这时先找到被删除节点的右子树最小节点并删除它,将访问节点继续入栈。
再依次检查栈顶节点的平衡状态和修正直到栈空。
对于删除操作造成的非平衡状态的修正,可以这样理解:对左或者右子树的删除操作相当于对右或者左子树的插入操作,然后再对应上插入的四种情况选择相应的旋转就好了。
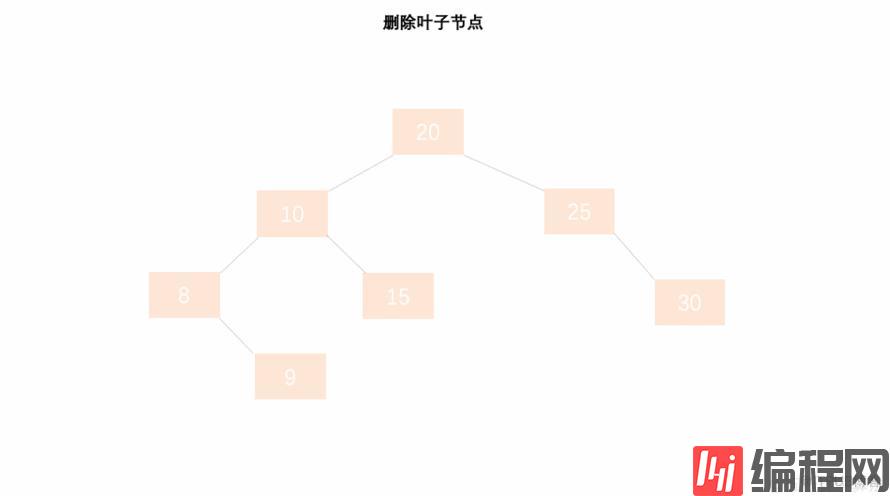
7.1 删除叶子节点
处理步骤:
①、将该节点直接从树中删除;
②、其父节点的子树高度的变化将导致父节点平衡因子的变化,通过向上检索并推算其父节点是否失衡;
③、如果其父节点未失衡,则继续向上检索推算其父节点的父节点是否失衡…如此反复②的判断,直到根节点 ;如果向上推算过程中发现了失衡的现象,则进行 ④ 的处理;
④、如果其父节点失衡,则判断是哪种失衡类型 [LL、LR、RR、RL] ,并对其进行相应的平衡化处理。如果平衡化处理结束后,发现与原来以父节点为根节点的树的高度发生变化,则继续进行 ② 的检索推算;如果与原来以父节点为根节点的高度一致时,则可说明父节点的父节点及祖先节点的平衡因子将不会有变化,因此可以退出处理;

具体数字演示:
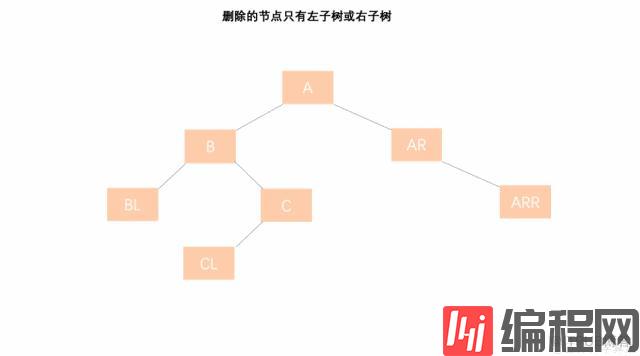
7.2 & 7.3 删除的节点只有左子树或右子树
处理步骤:
①、将左子树(右子树)替代原有节点 C 的位置;
②、节点 C 被删除后,则以 C 的父节点 B 为起始推算点,依此向上检索推算各节点(父、祖先)是否失衡;
③、如果其父节点未失衡,则继续向上检索推算其父节点 的父节点 是否失衡…如此反复 ② 的判断,直到根节点 ;如果向上推算过程中发现了失衡的现象,则进行 ④ 的处理;
④、如果其父节点失衡,则判断是哪种失衡类型 [LL、LR、RR、RL] ,并对其进行相应的平衡化处理。如果平衡化处理结束后,发现与原来以父节点为根节点的树的高度发生变化,则继续进行 ② 的检索推算;如果与原来以父节点为根节点的高度一致时,则可说明父节点的父节点及祖先节点的平衡因子将不会有变化,因此可以退出处理;
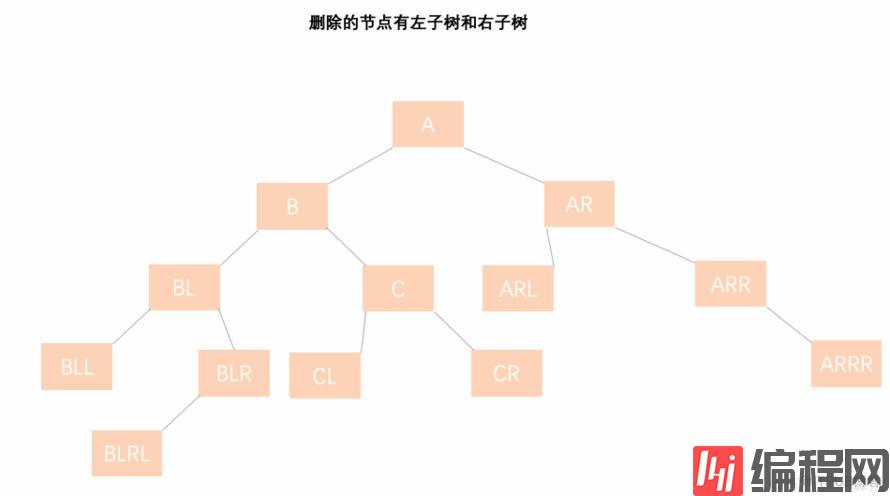
7.4 删除的节点既有左子树又有右子树
处理步骤:
①、找到被删节点 B 和替代节点 BLR (节点 B 的前继节点或后继节点 —— 在此选择 前继);
②、将替代节点 BLR 的值赋给节点 B ,再把替代节点 BLR 的左孩子 BLRL 替换替代节点 BLR 的位置;
③、以 BLR 的父节点 BL 为起始推算点,依此向上检索推算父节点或祖先节点是否失衡;
④、如果其父节点未失衡,则继续向上检索推算其父节点的父节点是否失衡…如此反复③的判断,直到根节点;如果向上推算过程中发现了失衡的现象,则进行⑤的处理;
⑤、如果其父节点失衡,则判断是哪种失衡类型 [LL、LR、RR、RL] ,并对其进行相应的平衡化处理。如果平衡化处理结束后,发现与原来以父节点为根节点的树的高度发生变化,则继续进行 ② 的检索推算;如果与原来以父节点为根节点的高度一致时,则可说明父节点的父节点及祖先节点的平衡因子将不会有变化,因此可以退出处理;
看完上述内容是否对您有帮助呢?如果还想对相关知识有进一步的了解或阅读更多相关文章,请关注编程网行业资讯频道,感谢您对编程网的支持。




