粒子群优化算法（PSO）python实践

1 算法介绍和原理

1.1 算法原理

强烈推荐知乎大佬的这篇文章：粒子群优化算法(Particle Swarm Optimization, PSO)的详细解读 - 知乎 (zhihu.com)。该文章详细介绍了算法的原理、算法流程、参数解释和一些Tips，这里就不过多赘述了。

粒子群优化算法（PSO, Particle Swarm Optimization），属于启发式算法中的一种，常用于多目标优化，寻找全局最优解，具有收敛速度快、参数少、算法简单的优点。

算法流程图如下（图片来自这篇文章）：

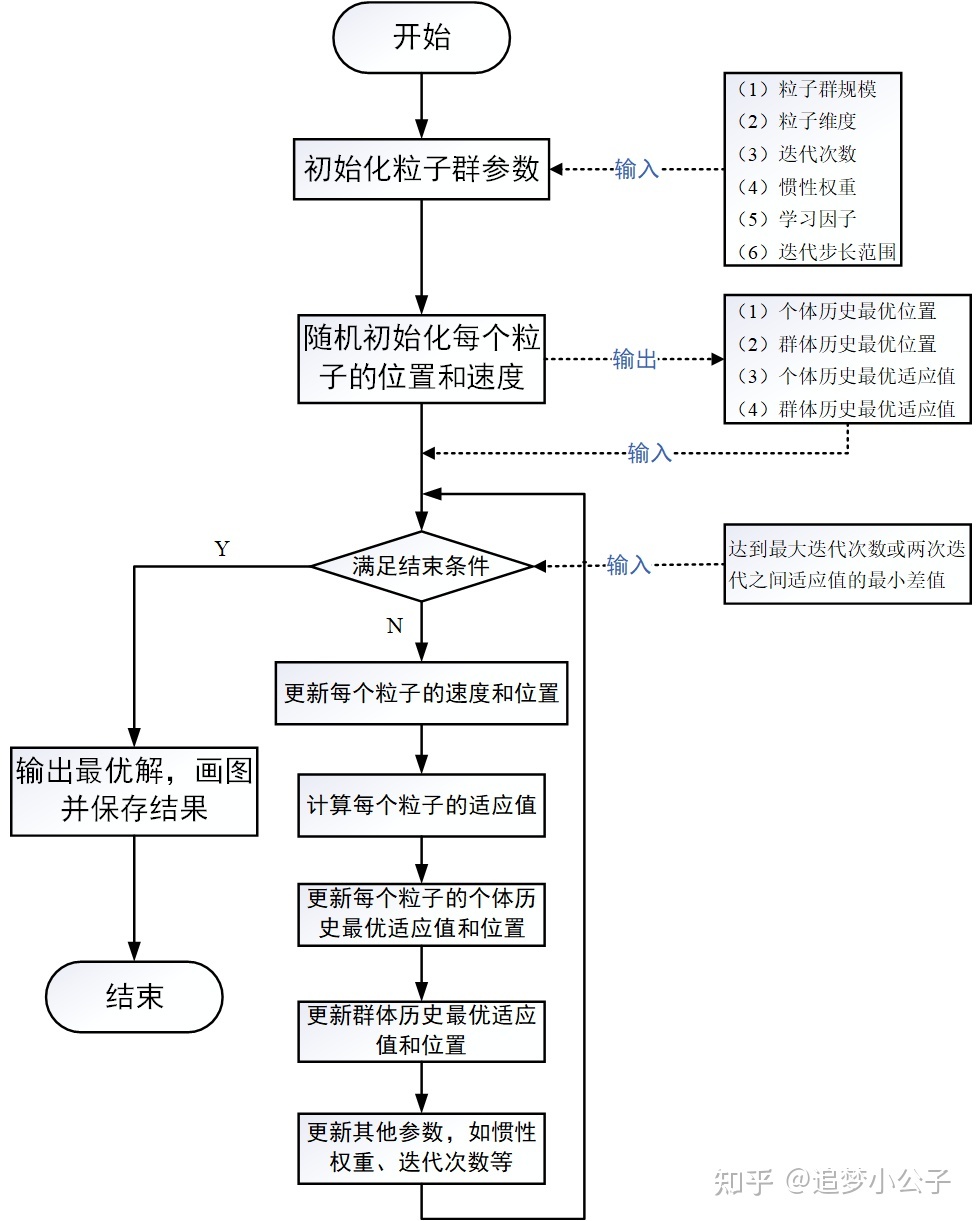
1.2 更新公式

1.2.1 速度更新公式

$$v_{id}^{k+1}=\omega v_{id}^k+c_1{r}_1\left(p_{id,\text{ pbest }}^k-x_{id}^k\right)+c_2{r}_2\left(p_{d,\text{ gbest }}^k-x_{id}^k\right)$$

$v_{id}^{k+1}$ —— 粒子 $i$ 在第 $k$ 次迭代中第 $d$ 维的速度向量。

$p_{id,\text{ pbest }}^k$ —— 粒子 $i$ 在第 $k$ 次迭代中第 $d$ 维的历史最优位置。

速度可以看作一个向量，具有大小和方向。即是粒子下一轮迭代移动的距离和方向。公式分为三部分，第一部分为惯性项，由该粒子的当前速度和惯性权重 $\omega$ 组成。第二部分为认知项，即是粒子当前位置和自身历史最优位置间的距离和方向。 第三部分为社会项，即是粒子当前位置和群体历史最优位置间的距离和方向。

对于更新速度的方向，等于三部分向量和向量的方向。

1.2.2 位置更新公式

$$x_{id}^{k+1}=x_{id}^k+v_{id}^{k+1}$$

点加向量等于点

大致掌握算法原理后，直接上手代码。

2 代码实现

示例问题：

求解如下函数的极小值
$$y=x_1{e}^{x_2}+x_{3}sin{x}_2+x_4{x}_5$$
每个变量的取值都在(1,25)。

首先是定义一个求解类及其初始化方法。

class PSO:    def __init__(self, D, N, M, p_low, p_up, v_low, v_high, w = 1., c1 = 2., c2 = 2.):        self.w = w  # 惯性权值        self.c1 = c1  # 个体学习因子        self.c2 = c2  # 群体学习因子        self.D = D  # 粒子维度        self.N = N  # 粒子群规模，初始化种群个数        self.M = M  # 最大迭代次数        self.p_range = [p_low, p_up]  # 粒子位置的约束范围        self.v_range = [v_low, v_high]  # 粒子速度的约束范围        self.x = np.zeros((self.N, self.D))  # 所有粒子的位置        self.v = np.zeros((self.N, self.D))  # 所有粒子的速度        self.p_best = np.zeros((self.N, self.D))  # 每个粒子的最优位置        self.g_best = np.zeros((1, self.D))[0]  # 种群（全局）的最优位置        self.p_bestFit = np.zeros(self.N)  # 每个粒子的最优适应值        self.g_bestFit = float('Inf')  # float('-Inf')，始化种群（全局）的最优适应值，由于求极小值，故初始值给大，向下收敛，这里默认优化问题中只有一个全局最优解        # 初始化所有个体和全局信息        for i in range(self.N):            for j in range(self.D):                self.x[i][j] = random.uniform(self.p_range[0][j], self.p_range[1][j])                self.v[i][j] = random.uniform(self.v_range[0], self.v_range[1])            self.p_best[i] = self.x[i]  # 保存个体历史最优位置，初始默认第0代为最优            fit = self.fitness(self.p_best[i])            self.p_bestFit[i] = fit  # 保存个体历史最优适应值            if fit < self.g_bestFit:  # 寻找并保存全局最优位置和适应值                self.g_best = self.p_best[i]                self.g_bestFit = fit

然后定义适应度计算函数，也就是我们要寻优的对象。

def fitness(x):    """    根据粒子位置计算适应值，可根据问题情况自定义    """    return x[0] * np.exp(x[1]) + x[2] * np.sin(x[1]) + x[3] * x[4]

定义每次迭代的更新函数。

def update(self):    for i in range(self.N):        # 更新速度(核心公式)        self.v[i] = self.w * self.v[i] + self.c1 * random.uniform(0, 1) * (                self.p_best[i] - self.x[i]) + self.c2 * random.uniform(0, 1) * (self.g_best - self.x[i])        # 速度限制        for j in range(self.D):            if self.v[i][j] < self.v_range[0]:                self.v[i][j] = self.v_range[0]            if self.v[i][j] > self.v_range[1]:                self.v[i][j] = self.v_range[1]        # 更新位置        self.x[i] = self.x[i] + self.v[i]        # 位置限制        for j in range(self.D):            if self.x[i][j] < self.p_range[0][j]:                self.x[i][j] = self.p_range[0][j]            if self.x[i][j] > self.p_range[1][j]:                self.x[i][j] = self.p_range[1][j]        # 更新个体和全局历史最优位置及适应值        _fit = self.fitness(self.x[i])        if _fit < self.p_bestFit[i]:            self.p_best[i] = self.x[i]            self.p_bestFit[i] = _fit        if _fit < self.g_bestFit:            self.g_best = self.x[i]            self.g_bestFit = _fit

其中主要完成每轮迭代中单个粒子位置和速度，历史最优位置和最优适应度的更新，以及群体（全局）的最优位置和最优适应度的更新。

最后，便是主要函数的实现。

def pso(self, draw = 1):    best_fit = []  # 记录每轮迭代的最佳适应度，用于绘图    w_range = None    if isinstance(self.w, tuple):        w_range = self.w[1] - self.w[0]        self.w = self.w[1]    time_start = time.time()  # 记录迭代寻优开始时间    for i in range(self.M):        self.update()  # 更新主要参数和信息        if w_range:            self.w -= w_range / self.M  # 惯性权重线性递减        print("\rIter: {:d}/{:d} fitness: {:.4f} ".format(i, self.M, self.g_bestFit, end = '\n'))        best_fit.append(self.g_bestFit.copy())    time_end = time.time()  # 记录迭代寻优结束时间    print(f'Algorithm takes {time_end - time_start} seconds')  # 打印算法总运行时间，单位为秒/s    if draw:        plt.figure()        plt.plot([i for i in range(self.M)], best_fit)        plt.xlabel("iter")        plt.ylabel("fitness")        plt.title("Iter process")        plt.show()

测试代码如下。

if __name__ == '__main__':    low = [1, 1, 1, 1, 1]    up = [25, 25, 25, 25, 25]    pso = PSO(5, 100, 50, low, up, -1, 1, w = 0.9)    pso.pso()

测试结果如下图所示。

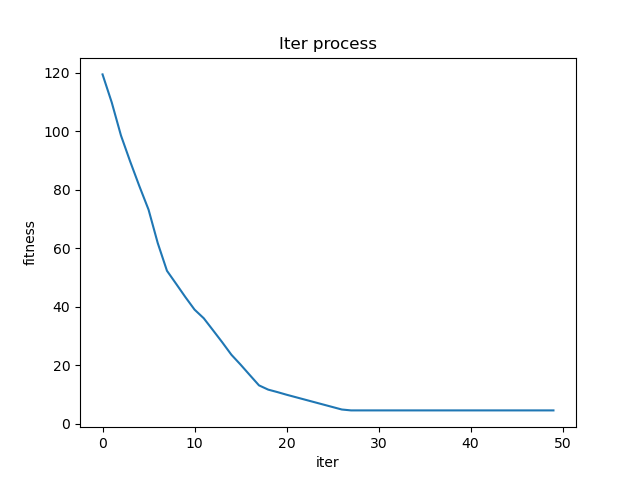
...Iter: 47/50 fitness: 4.5598 Iter: 48/50 fitness: 4.5598 Iter: 49/50 fitness: 4.5598 Algorithm takes 0.1444549560546875 seconds

可以看到在第30轮就已经完全收敛了，且函数在求解空间中的极小值为4.5598。

3 总结

• 动态的惯性权重${}^{[1]}$

  

  w_range = self.w[1] - self.w[0]self.w = self.w[1]self.w -= w_range / self.M  # 惯性权重线性递减

• fitness变化逻辑

  fitness是适应度函数值，通常问题是寻找解空间内的粒子，使得该粒子所代表的解的fitness向下或向上收敛于某一定值。对于不同收敛方向，个体和全局最优fitness一般初始化赋值无穷大或者无穷小float('Inf')/float('-Inf')。并且在判断更新最优适应值时也应当注意大小于符号。

• 程序复用

  对于上面的PSO类代码，不同多元寻优问题均可通过重写类中的fitness函数实现。或者定义self.fitness_function属性进行外部函数名传参赋值。

参考

[1] 粒子群优化算法(Particle Swarm Optimization, PSO)的详细解读 - 知乎 (zhihu.com)

[2] 粒子群算法(PSO)的Python实现（求解多元函数的极值）_Cyril_KI的博客-CSDN博客_pso算法python

来源地址：https://blog.csdn.net/qq_39784672/article/details/127750401