目录
一、逻辑回归简介及应用
logistic回归又称logistic回归分析,是一种广义的线性回归分析模型,常用于数据挖掘,疾病自动诊断,经济预测等领域。例如,探讨引发疾病的危险因素,并根据危险因素预测疾病发生的概率等。以胃癌病情分析为例,选择两组人群,一组是胃癌组,一组是非胃癌组,两组人群必定具有不同的体征与生活方式等。因此因变量就为是否胃癌,值为“是”或“否”,自变量就可以包括很多了,如年龄、性别、饮食习惯、幽门螺杆菌感染等。然后通过logistic回归分析,可以得到自变量的权重,同时根据该权值可以根据危险因素预测一个人患癌症的可能性。
Logistic回归的因变量可以是二分类的,如上述中是否患胃癌;也可以是多分类的,如mnist手写识别,但是二分类的更为常用,也更加容易解释。所以实际中最常用的就是二分类的Logistic回归。
二、逻辑回归的原理
谈到回归问题,第一反应是: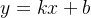 在二维平面上是一条直线。当
在二维平面上是一条直线。当 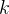 和
和 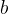 确定时,对于回归问题,假设
确定时,对于回归问题,假设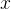 为面积,经过线性映射,可以得到其体积
为面积,经过线性映射,可以得到其体积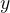 ,则完成回归任务;对于分类问题,假设
,则完成回归任务;对于分类问题,假设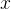 为某个特征,经过线性映射,得到
为某个特征,经过线性映射,得到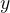 >0,或<0,或=0,若规定大于0的为正标签,小于等于0的为负标签,则完成了分类任务。
>0,或<0,或=0,若规定大于0的为正标签,小于等于0的为负标签,则完成了分类任务。
同理可得,当方程为多元方程时: 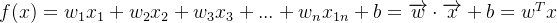 ,如下图所示:
,如下图所示:

如果继续对多元方程回归得到的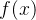 规定大于0的为正标签,小于等于0的为负标签。由于
规定大于0的为正标签,小于等于0的为负标签。由于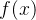 的值域为
的值域为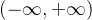 ,这样规定对于决策很不友好;若
,这样规定对于决策很不友好;若![f(w)\in \left [ 0,1 \right ]](https://file.lsjlt.com/upload/f/202310/02/dn1v3f01djh.png) ,规定大于阈值0.5为正标签,小于等于阈值0.5为负标签,那么越比0.5大,就越说明决策函数给出的正类的可信度越高,反之亦然。这样不仅灵活,而且可以根据数据情况调整不同的阈值来达到最佳准召率。
,规定大于阈值0.5为正标签,小于等于阈值0.5为负标签,那么越比0.5大,就越说明决策函数给出的正类的可信度越高,反之亦然。这样不仅灵活,而且可以根据数据情况调整不同的阈值来达到最佳准召率。
(1)sigmoid函数
输入数据,经过函数映射为
![\left [ 0\sim 1 \right ]](https://file.lsjlt.com/upload/f/202310/02/al2e3sq0pum.png) ,该函数为sigmoid函数,形式为
,该函数为sigmoid函数,形式为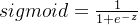
(2)输入和输出形式
输入:
输出: 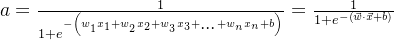 ,其中
,其中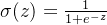
这里 和
和 如图所示,分别为输入数据和待求参数,
如图所示,分别为输入数据和待求参数,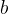 为偏置项,为了后续推导方便,设定:
为偏置项,为了后续推导方便,设定:,即
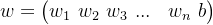 ,
,。
输出值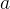 就是概率值,对
就是概率值,对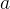 中参数
中参数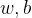 的求导过程如下所示,后面会用到,先求出来放在这里哈:
的求导过程如下所示,后面会用到,先求出来放在这里哈:
求导过程为除法求导运算法则,需要注意一个推导公式: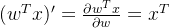 。
。
(3)基于目标函数求解参数w
极大似然估计提供了一种基于给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。简单说来,就是知道了模型和结果,求解使得事件结果以最大概率发生时出现的参数。
基于逻辑回归的计算式,对应标签1和0的概率分别为: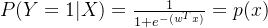
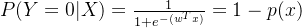
第一步,构造极大似然函数,计算这些样本的似然函数,其实就是把每个样本的概率乘起来,
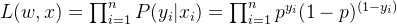
第二步,两边取对数得: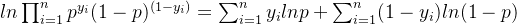
tips:由于极大似然函数中有连乘符号,取对数,将连乘变为加和。
目标函数为: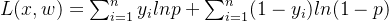 其中,y为真值,p为预测值。
其中,y为真值,p为预测值。
原函数求最大值,等价于乘以负1后求最小值。对于n个数据累加后值较大,用梯度下降容易导致梯度爆炸,可处于样本总数n,即
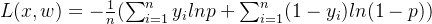
第三步,对目标函数中参数w求导:为了求导过程更清晰,先去掉求和符号
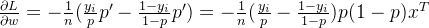
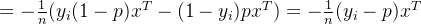
tips: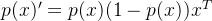 ,该求导过程,涉及到对概率值p的求导,这个求导过程在前面已经推导完成。
,该求导过程,涉及到对概率值p的求导,这个求导过程在前面已经推导完成。
添加求和符号后为: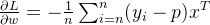
基于梯度下降法求得最优w: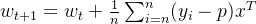
三、逻辑回归代码复现
后续补充。
参考文献:
【大道至简】机器学习算法之逻辑回归(Logistic Regression)详解(附代码)---非常通俗易懂!
来源地址:https://blog.csdn.net/qq_25993375/article/details/129675047




