本篇内容介绍了“C++如何实现二叉树的遍历”的有关知识,在实际案例的操作过程中,不少人都会遇到这样的困境,接下来就让小编带领大家学习一下如何处理这些情况吧!希望大家仔细阅读,能够学有所成!
二叉树的遍历
Q:什么是二叉树的遍历?
A:二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次,且仅被访问一次。
Q:二叉树有几种遍历方法?
A:二叉树的遍历方法可以有很多种,如果限制了从左到右的习惯方式,那么主要分为以下四种:先序遍历,中序遍历,后序遍历,层序遍历。
前序遍历
Q:什么是先序遍历
A:先序遍历就是先访问树的根节点,再访问树的左子节点,再访问右子节点。可以想象为,从一棵二叉树根节点为起点,沿着二叉树外沿,逆时针走一圈回到根节点,路上遇到的元素顺序,就是先序遍历的结果。
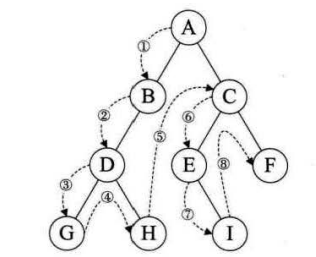
如图:遍历的顺序为 ABDGHCEIF
操作定义
若二叉树为空,则空操作返回,否则:
访问根节点
先序遍历左子树
先序遍历右子树
代码演示
void PreOrderTraversal(BiTree BT){ if( BT != NULL ) { printf(“%d\n”, BT->Data); //对节点的数据进行打印 PreOrderTraversal(BT->Left); //访问左子树 PreOrderTraversal(BT->Right); //访问右子树 }}中序遍历
Q:什么是中序遍历
A:中序遍历就是访问完所有左子数后再访问根节点,最后访问右子树,即左子树-根节点-右子树。中序遍历可以看成,二叉树每个节点,垂直方向投影下来,然后从左往右数,得出的结果便是中序遍历的结果。
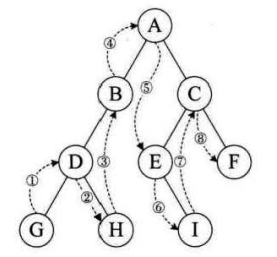
如图:遍历的顺序为GDHBAECF
操作定义
若二叉树为空,则空操作返回,否则:
中序遍历左子树
访问根节点
中序遍历右子树
代码演示
void InOrderTraversal(BiTree BT){ if(BT) { InOrderTraversal(BT->Left); printf("%d\n", BT->Data); InOrderTraversal(BT->Right); }}后序遍历
Q:什么后序遍历
A:后序遍历就是先访问左子树和右子树,最后访问节点,即左子树-右子树-根节点。后序遍历可以看成围着树的外围绕一圈,若下面只有一个结点就摘下来,得出的结果便是后序遍历的结果。
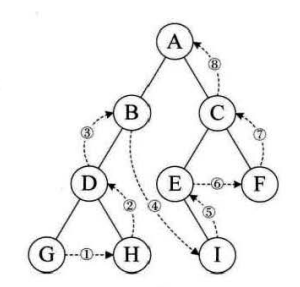
如图:遍历的顺序为GHDBIEFCA
操作定义
若二叉树为空,则空操作返回,否则:
后序遍历左子树
后序遍历右子树
访问根节点
代码演示
void PostOrderTraversal(BiTree BT){ if (BT) { PostOrderTraversal(BT->Left); PostOrderTraversal(BT->Right); printf("%d\n", BT->Data); }}层序遍历
Q:什么层序遍历
A:层次遍历就是从根节点开始,一层一层,从上到下,每层从左到右,依次取值。
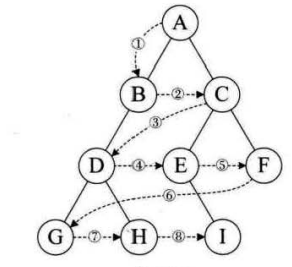
如图:遍历的顺序为ABCDEFGHL
代码演示
void LevelOrder(BiTree T){InitQueue(Q);//初始化辅助队列BiTree p;EnQueue(Q,T);//将根结点入队while(!IsEmpty(Q)){//队列不空则循环DeQueue(Q,p);//队头结点出队visit(p);//访问出队结点if(p->1child!=NULL)EnQueue(Q,p->lchild);//左子树不空,则左子树根结点入队if(p->rchild!=NULL)EnQueue(Q,p->rchild);//右子树不空,则右子树根结点入队}}“C++如何实现二叉树的遍历”的内容就介绍到这里了,感谢大家的阅读。如果想了解更多行业相关的知识可以关注编程网网站,小编将为大家输出更多高质量的实用文章!





