小编给大家分享一下python中PTD算法的示例分析,相信大部分人都还不怎么了解,因此分享这篇文章给大家参考一下,希望大家阅读完这篇文章后大有收获,下面让我们一起去了解一下吧!
1.引言
1.1什么是地面点滤波?
机载激光雷达(airborne light detection and ranging)/机载激光扫描(ALS, airborne laser scanning)在过去20多年的时间里迅速发展,其相对于传统摄影测量影像及INSAR(干涉合成孔径雷达)可以直接记录从地物或地表返回的密集、离散、细节丰富、精确的三维点云。如何对这些不规则点云进行处理应用是我们要解决的问题,其中一个重要的处理步骤就是:地面点滤波(ground filterring),简而言之就是“在无序、不规则的三维离散点云中找到哪些是由地表返回的,哪些是由地物返回的。”
注:关于地面点滤波的概念我们要与孤立点(outlier)滤波区分开,孤立点滤波可以理解为图像中的去噪,去除数据测量过程中受到飞鸟、多路径效应所产生的远低于/高于其他数据的点。
1.2地面点滤波的相关方法
众多学者已经提出了各种类型的滤波算法来从ALS三维点云中自动提取地面点,根据滤波器的概念可以分为以下四类:
slope-based
block-minimum
surface-based
clustering/segmentation algorithm
基于面的地面点滤波方法的核心步骤是创建一个最接近裸露地表的表面,其使用了更多的context(上下文,环境、背景)信息,所以一般可以取得比其他滤波方法更好的滤波效果。此外,根据创建表面的方法又可以把surface-based类型滤波器分为以下三个子类:
Morphology-based filters
Iterative-interpolation-based filters
Progressive-densification-based filters
其中Morphology-based filters使用不同尺寸大小的窗口形态学操作(opening/geodesic)来去除不同大小的地物,但是这类方法需要假设地形的坡度是一个常数。以及面临着一个巨大的挑战是在窗口大小变化的时候怎么保持地形特征不变;Iterative-interpolation-based filters是通过整个点云数据集来逐步接近地表,首先通过一个粗糙的表面来计算点云到表面的残差,通常来说地物点会有正的差值,地面点会有负的差值。这种方法最大的挑战是当精度一定的条件下怎么来提高算法的效率;Progressive-densification-based filters与上一种方法类似,也是渐进地把每个点逐步的分类为地面点,然而此方法不需要进行插值。本篇博客中所介绍的PTD(progressive TIN densification)就是属于surface-based类型中的一种Progressive-densification-based filters。
2.PTD具体介绍
PTD是Axelsson在2000年左右提出的一种经典滤波方法,在工程应用(TerraScan)及科学社区中得到了广泛的应用。主要可以通过以下五个步骤进行实现:
2.1去除孤立点
如引言中1.1所述,去除孤立点类似于图像中的去噪操作。outliers是测量数据集中的那些远高于/低于地表的点,这中情况常常会导致滤波算法出现错误(例如,PTD算法中假设格网中的最低点为地面点,从而导致错误)。可以通过下述三个简单步骤来去除孤立点,当然除此之外还有其他很多更加优秀的方法。
对所有数据的高程进行统计,建立一个高程分布的直方图,通过观察高程分布来确定高程阈值,从而消除分布中最低和最高的小“尾巴”。
通过每个点与周围点之间的最小高程差来进行搜寻仍然存在的孤立点(这里使用一个2D的KD树来进行组织查询每个点的近邻点)。
手工校正孤立点自动去除过程中所产生的错误。
2.2参数说明
在PTD算法中有以下6个参数进行预先设置:
1)最大建筑尺寸m:m是一个长度阈值,此阈值被用来定义格网的大小,随后算法可以处理建筑物尺寸小于此阈值的建筑物。
2)最大地形角度t:t是一个坡度阈值,决定了通过什么方式(是否进行设置镜像点)去判断未分类点的类别。如果未分类点所在三角面的坡度大于t则应该通过一个镜像点来进行判断,反之则直接判断。(后续在2.4中也会再进行详细介绍)。
3)最大角度θ:θ是三角面与待分类点和最近的三角网顶点之间连线之间的最大角度。如果一个未分类点对应的角度大于θ则被标记为地物点,否则设置为地面点。
4)最大距离d:d是当前迭代中从待判断点到三角面之间的最大距离,类似的,如果一个未分类点对应的最大距离大于d则被标记为地物点,否则设置为地面点。
5)最小边长l:l是构建TIN模型中所有三角形最长边(平面投影)的最小阈值。当三角形中的所有边都小于l时,则停止在三角网中加入地面点(注意l是在平面中计算的)。因此,此参数可以避免引起地面模型中过高的点密度,以及降低内存的使用。
6)最大边长l':*l'是构建TIN模型中所有三角形最短边(平面投影)的最大阈值,当三角形中的所有边都小于l'*被用于停止处理处理三角形。因此,此参数用于稀疏地面点,以及降低内存的使用。
2.3选择种子点并构建TIN模型
对给定的点云数据集定义一个特定的“bounding box”并固定左上角坐标(xtopleft, ytopleft)右下角坐标(xbottomright, ybottomright),宽度w,以及高度h。然后通过上述定义的变量通过以下公式把整个数据区域划分成nRow行,nColumn列,尺寸大小为m的格网。
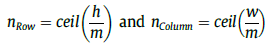
其中m,为最大建筑尺寸,ceil(x)函数代表向上取整,即找到不小于x的最小整数。
根据整个数据集划分为格网之后,每个网格中的最低点被设置为“种子点”(初始地面点)。除此之外,“bounding box”的四个角点也被设置为“种子点”(其高程值等同于距离最近的种子点高程),如下图所示:
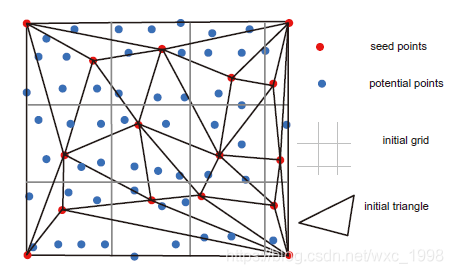
注:把“bounding box”的四个角点也被设置为“种子点”是为了保证所有点都处于TIN模型内部。
随后,根据选择好的种子点来构建初始TIN模型来表示初始地表,剩余的点被默认标记为地物。
2.4迭代加密TIN模型
在每次迭代过程中通过预先设置的阈值参数,来对“潜在点(potential point)”进行逐点判断。详细步骤如下所述:
1)确定潜在点(potential point)的所在位置PPotential(xp,yp,zp),找到其所在的三角形Ttriangle,即PPotential在三角形内部或边缘上或者在顶点上。
2)计算三角平面的坡度Striangle,如果Striangle小于预先设置的最大地形角度t,则进行第3)步,若大于则进行第4)步。
3)如下图所示,计算的两个参数,包括:三角面Ttriangle与待分类点PPotential和最近的三角网顶点之间连线之间的角度,表示为Aangle,以及待分类点PPotential和三角面Ttriangle之间的距离,表示为Ddistance。如果PPotential所对应的上述两个参数Aangle小于最大角度θ,Ddistance小于最大距离d则认为待分类点PPotential是地面点,否则认为是地物点。随后,进行下一个点的判断。
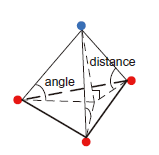
4)如果三角平面的坡度Striangle大于预先设置的最大地形角度t则需要设置PPotential的镜像点。先找到PPotential所在三角形
Ttriangle中高程值最大的顶点Pvertex(xv,yv,zv),然后通过下式计算PPotential的镜像点:
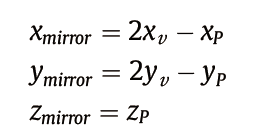
其中(xmirror,ymirror,zmirror)是所求镜像点的三维坐标。
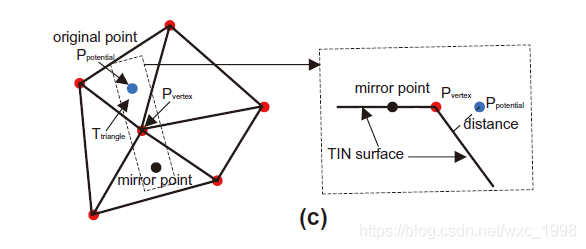
接着对镜像点使用步骤3)的方式来进行计算Aangle与Ddistance两个参数进行判断,来决定PPotential的类别。
5)在结束每次迭代之后,新检测出的地面点通过下述步骤加入TIN模型中。
确定Pground(xg,yg,zg)的坐标,找到其所在的三角形T'triangle。
计算三角形T'triangle的所有边在水平投影中的长度,如果任意边的长度都大于l加入当前地面点Pground到TIN模型中,并进行刷新。否则,进行判断下一个新检测的地面点。
重复上述迭代,直到不再有点被加入到地面点集中。
上述五个步骤就是PTD算法的主要实现方法了,PTD算法已经被广泛应用在各种类型的景观(地形)中,且取得不错的效果。但是需要注意的是,虽然在算法中采用了设置“镜像点”的方式来避免出现cutting-off的问题(断裂线分布区域),其还是对陡峭地形非常敏感。
以上是“python中PTD算法的示例分析”这篇文章的所有内容,感谢各位的阅读!相信大家都有了一定的了解,希望分享的内容对大家有所帮助,如果还想学习更多知识,欢迎关注编程网行业资讯频道!




