基于Python如何实现模拟三体运动

本文小编为大家详细介绍“基于Python如何实现模拟三体运动”，内容详细，步骤清晰，细节处理妥当，希望这篇“基于Python如何实现模拟三体运动”文章能帮助大家解决疑惑，下面跟着小编的思路慢慢深入，一起来学习新知识吧。

拉格朗日方程

此前所做的一切三体和太阳系的动画，都是基于牛顿力学的，而且直接对微分进行差分化，从而精度非常感人，用不了几年就得撞一起去。

为了给三体人提供一个更加有价值的推导，这次通过求解拉格朗日方程的数值解来实现。

首先假设三个质点的质量分别为m₁, m₂,m₃,坐标为x^→₁,x^→₂,x^→₃,质点速度可以表示为x ^→ ˙.假设三体在二维平面上运动，则第i个质点的动能为

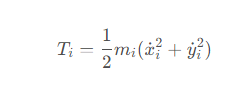
引力势能为

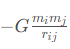
其中G为万有引力常量，r_ij为质点i,j之间的距离，则系统的拉格朗日量为

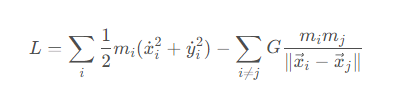
有了拉格朗日量，将其带入拉格朗日方程

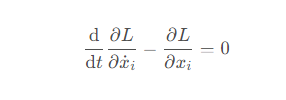
就可以得到拉格朗日方程组。

推导方程组

对于三体系统而言，总计有3个粒子，每个粒子有x,y两个自由度，也就是说最后会得到6组方程。考虑到公式推导过程中可能会出现错误，所以下面采用sympy来进行公式推导。

首先定义符号变量

from sympy import symbolsfrom sympy.physics.mechanics import dynamicsymbolsm = symbols('m1:4')x = dynamicsymbols('x1:4')y = dynamicsymbols('y1:4')

接下来，需要构造系统的拉格朗日量L，其实质是系统的动能减去势能，对于上面构建的三体系统而言，动能和势能可分别表示为

计算每个质点的动能和势能。动能是由速度决定的，而速度是由位置对时间的导数决定的。我们可以用 sympy 的 diff 函数来求导：

from sympy import diff# 此为速度的平方v2 = [diff(x[i],t)**2 + diff(y[i])**2 for i in range(3)]T = 0for i in range(3):    T += m[i]*v2[i]/2

势能是由万有引力决定的，而万有引力是由两个质点之间的距离决定的。我们可以用 sympy 的 sqrt 函数来求距离：

from sympy import sqrt,cosG = symbols('G') # 引力常数ijs = [(0,1), (0,2),(1,2)]dij = [sqrt((x[i]-x[j])**2+(y[i]-y[j])**2) for i,j in ijs]U = 0for k in range(3):    i,j = ijs[k]    U -= G*m[i]*m[j]/dij[k]

有了动能和势能，就可以愉快地求拉格朗日量了，有了拉格朗日量，就可以列拉格朗日方程了

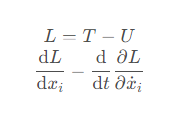
三个粒子的每一个坐标维度，都可以列出一组拉格朗日方程，所以总共有6个拉格朗日方程组

from sympy import solveL = T - UeqLag = lambda x : diff(L, x)-diff(diff(L, diff(x, t)), t)# 拉格朗日方程组eqs = [eqLag(xi) for xi in x+y]

记x_ij=x_i−x_j,y_ij=y_i−y_j ，则

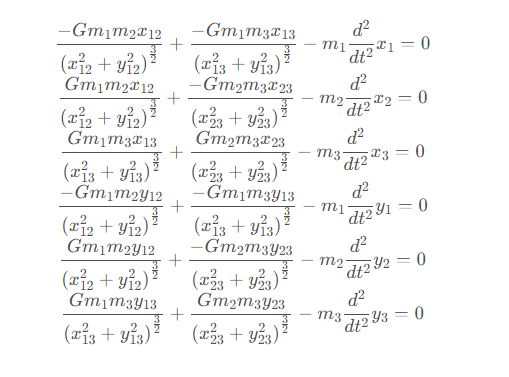
微分方程算法化

接下来就要调用Python的odeint来计算这个微分方程组的数值解，odeint的调用方法大致为odeint(func, y, t, args)，其中func是一个函数，这个函数必须为func(y,t,...)，且返回值为dy/dt.

为此，需要将上述方程组再行拆分，以消去其中的二次导数，以x1为例，令u1=dx1/dt ，则此方程变为方程组

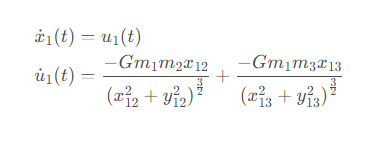
由于三体系统中有3个粒子，共6个独立变量，所以要列12个方程。记

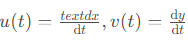
则odeint输入的y的形式为

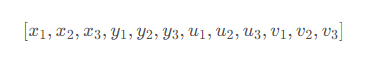
从而func的具体形式为

import numpy as npdxy = lambda x,y : np.sqrt(x**2+y**2)**(3/2)def triSys(Y, t, m, G):    jk = [(1,2),(0,2),(0,1)]    x,y = Y[:3], Y[3:6]    u,v = Y[6:9], Y[9:]    du, dv = [], []    for i in range(3):        j, k = jk[i]        xji, xki = x[j]-x[i], x[k]-x[i]        yji, yki = y[j]-y[i], y[k]-y[i]        dji, dki = dxy(xji, yji), dxy(yji, yki)        mji, mki = G*m[i]*m[j], G*m[i]*m[k]        du.append(mji*xji/dji + mki*xki/dki)        dv.append(mji*yji/dji + mki*yki/dki)    dydt = [*u, *v, *du, *dv]    return dydt

求解+画图

接下来就是见证奇迹的时刻，首先创建一个随机的起点，作为三体运动的初值，然后带入开整就完事儿了

from scipy.integrate import odeintnp.random.seed(42)y0 = np.random.rand(12)m = np.random.rand(3)t = np.linspace(0, 20, 1001)sol = odeint(triSys, y0, t, args=(m, 1))

然后绘制一下这三颗星的轨迹

import matplotlib.pyplot as pltplt.plot(sol[:,0], sol[:,3])plt.plot(sol[:,1], sol[:,4])plt.plot(sol[:,2], sol[:,5])plt.show()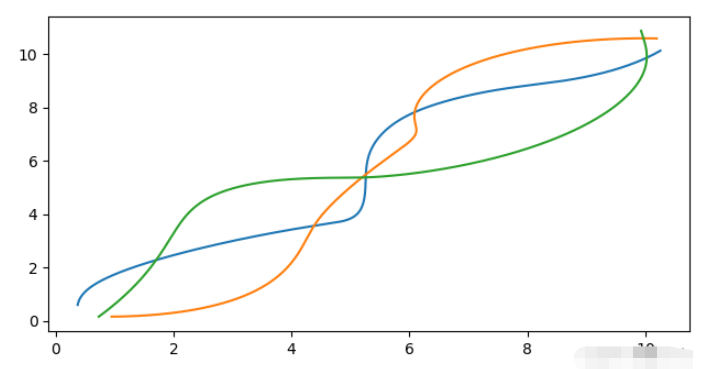

光是看这个轨迹就十分惊险了有木有。

如果把其中的第一颗星作为坐标原点，那么另外两颗星的轨迹大致为

plt.plot(sol[:,1]-sol[:,0], sol[:,4]-sol[:,3])plt.plot(sol[:,2]-sol[:,0], sol[:,5]-sol[:,3])plt.scatter([0],[0], c='g', marker='*')plt.show()

结果为

动图绘制

最后，以中间这颗星为原点，绘制一下另外两颗星运动的动态过程

import matplotlib.animation as animation fig = plt.figure(figsize=(9,4))ax = fig.add_subplot(xlim=(-1.8,1.8),ylim=(-1.8,1.5))ax.grid()traces = [ax.plot([],[],'-',lw=0.5)[0] for _ in range(2)]pts = [ax.plot([],[] ,marker='*')[0] for _ in range(2)]ax.plot([0],[0], marker="*", c='r')X1 = sol[:,1]-sol[:,0]Y1 = sol[:,4]-sol[:,3]X2 = sol[:,2]-sol[:,0]Y2 = sol[:,5]-sol[:,3]def animate(n):    traces[0].set_data(X1[:n], Y1[:n])    traces[1].set_data(X2[:n], Y2[:n])    pts[0].set_data([X1[n], Y1[n]])    pts[1].set_data([X2[n], Y2[n]])    return traces + ptsani = animation.FuncAnimation(fig, animate,     range(1000), interval=10, blit=True)ani.save('tri.gif')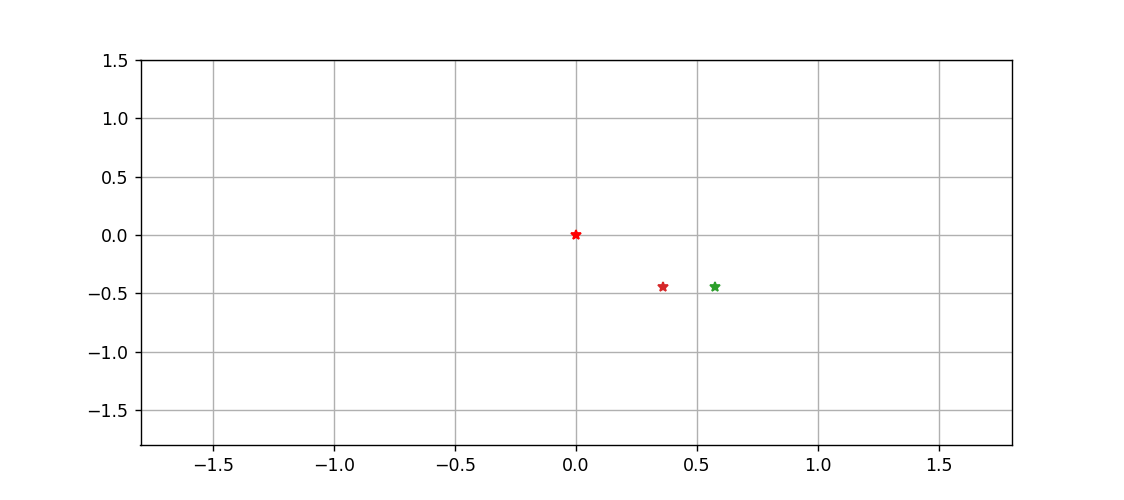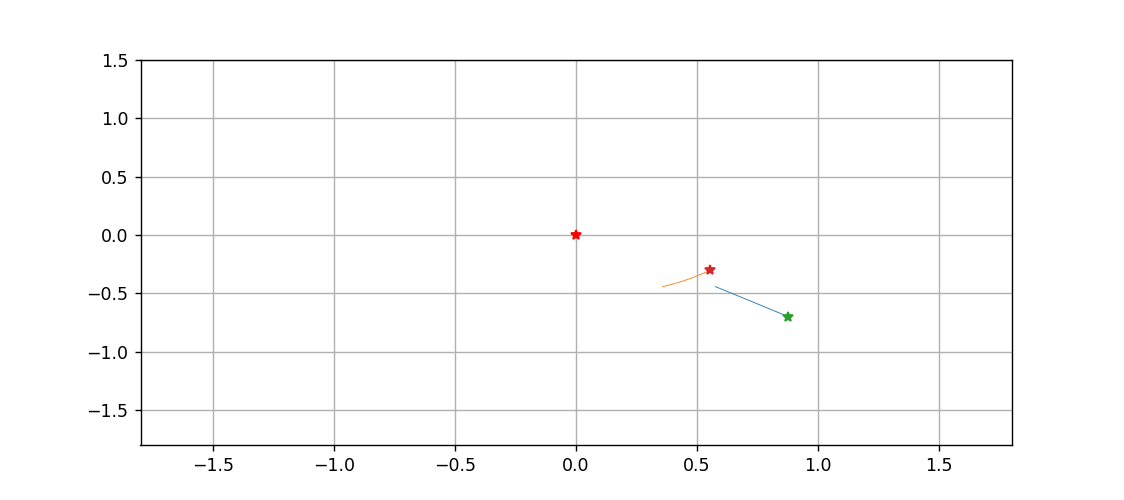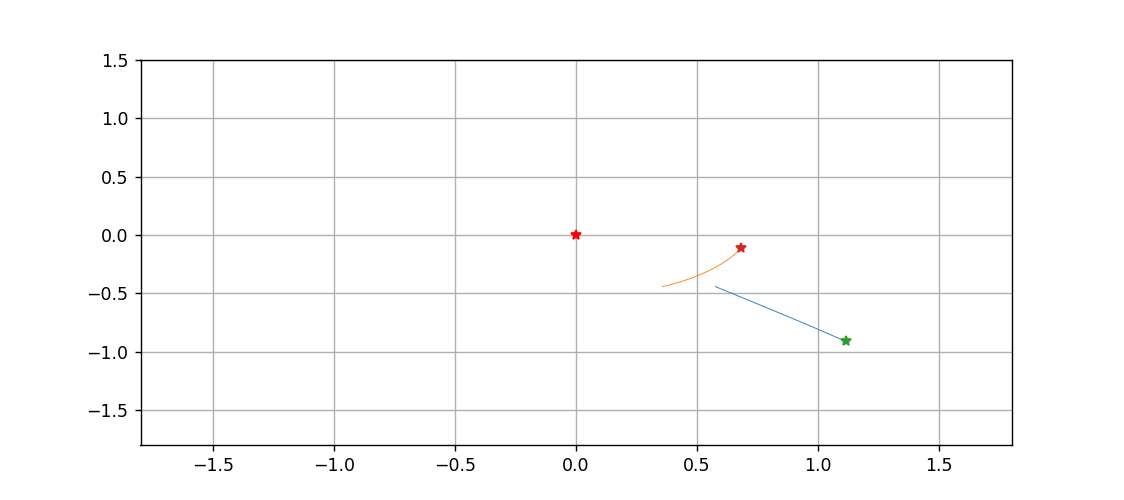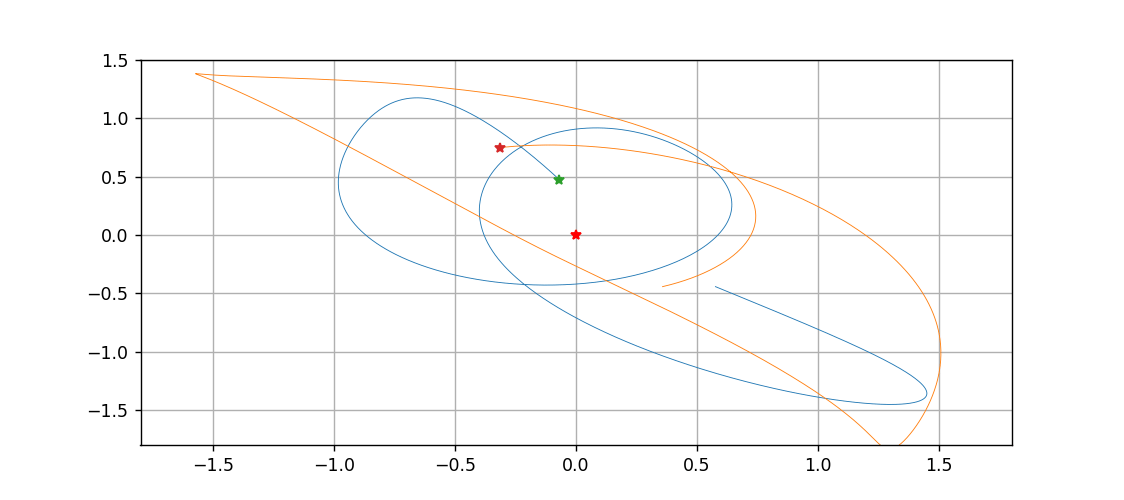

读到这里，这篇“基于Python如何实现模拟三体运动”文章已经介绍完毕，想要掌握这篇文章的知识点还需要大家自己动手实践使用过才能领会，如果想了解更多相关内容的文章，欢迎关注编程网行业资讯频道。