本篇文章来和大家一起探讨一下“香农定律和奈奎斯特基本准则”,文章虽不是很全面,但是内容都是精华,有需要的小伙伴,可以参考一下。一定要认真阅读哦!
(1)信道容量与香农定理(ShannonTheroy)
我们常常会遇到这样的问题:我的信道上到底可以传输多大的数据,或者指定的信道上的极限传输率是多少。这就是信道容量的问题。例如在xDSL系统中,我们使用的传输介质是仅有几兆带宽的电话线,而上面要传送几兆、十几兆甚至几十兆带宽的数据,如此高的速率能保证在几兆带宽的双绞线上可靠传输吗?或者说从另一个角度说,在给定通频带宽(Hz)的物理信道上,到底可以有多高的数据速率(b/S)来可靠传送信息?
早在半个多世纪以前,贝尔实验室的香农(ClaudeElwoodShannon)博士就已经解答这个问题。1948年,在《通信的数学原理》(MathematicalTheoryofCommunication)一文中,香农博士提出了著名的香农定理,为人们今天通信的发展垫定了坚实的理论基础。
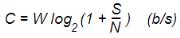
香农定理指出,在噪声与信号独立的高斯白噪信道中,假设信号的功率为S,噪声功率为N,信道通频带宽为W(Hz),则该信道的信道容量C有:
这就是香农信道容量公式。从公式(1)中我们可以看出,对于一定的信噪比和一定的传输带宽,它的传输速率的上限就确定了,这个极限是不能够突破的。由香农信道容量公式可得出以下结论:
(1)提高信道的信噪比或增加信道的带宽都可以增加信道容量。
(2)当信道中噪声功率N无穷趋于0时,信道容量C无穷趋于无限大,这就是说无干扰信道的信道容量可以为无穷大。
(3)信道容量C一定时,带宽W与信噪比S/N之间可以互换,即减小带宽,同时提高信噪比,可以维持原来信道容量。
(4)信噪比一定时,增加带宽W可以增大信道容量。但噪声为高斯白噪声时(实际的通信系统背景噪声大多为高斯白噪),增加带宽同时会造成信噪比下降,因此无限增大带宽也只能对应有限信道容量。
例1:有一个经调制解调器传输数据信号的电话网信道,该信道带宽为3000Hz,信道噪声为加性高斯白噪声,其信噪比为20db,求该信道的信道容量。
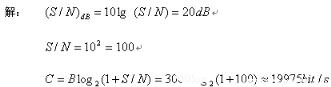
例2:已知仅存在加性高斯白噪声的信道容量为33.6Kbit/s,其信号噪声功率比为30db,求此模拟信道的带宽为多少?
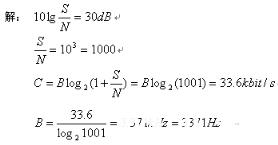
例3:考虑一个极端的噪声信道,其中信噪比近似于零。换言之,噪声很强使得信号很微弱。对于该信道,计算它的信道容量如下:
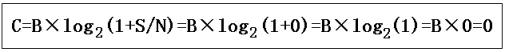
也就是说,该信道上噪声完全淹没了有效信号,在终端无法识别还原,因此该信道不适合传输数据,数据传输能力为0。
香农定理的伟大之处在于它的理论指导意义。香农公式给出频带利用的理论极限值,即在有限带宽、有噪声的信道中存在极限传输速率,无论采用何种编码都无法突破这个极限。另外香农定律还告诉我们,在信带容量一定的情况下,信噪比和带宽可以互换。比如航天技术中的宇际通信,由航天器发回的信号往往掩埋在比它高几十分贝的宇宙噪声之中,虽然信号非常微弱,但香农公式指出信噪比和带宽可以互换,只要信噪比在理论计算的范围内,我们总可以找到一种方法将有用信号恢复出来。另外,如移动通信中的多址接入技术(FDMA、TDMA、CDMA、SDMA以及OFDM),还有各种信源编码、信道传输编码、纠错编码技术等等,都得益于香农定理。在xDSL传送系统中,人们正是选择了合理的信道编码技术[微软用户1](DMT和CAP编码调制方式),可以保证信息在有限的通频带宽内可靠的传递,从而实现数据的高速传输,满足了人们宽带上网的需求。
奈奎斯特定律
奈奎斯特定律是一种信息速率,根据奈奎斯特定律,信道的极限速率(码元速率)等于信道带宽(低通信道)的2倍(理论状态)。
对于四进制信号,可以表示四种电平,这种情况下信息速率就是码元速率的两倍,就是可以传输4倍带宽信息速率。这就是编码方式。
对于理论上的无噪音线路,速率可以到达无穷大。
但实际上都是有噪音的,噪音的大小决定了各信号之间的电平差距。也就是到底可以有多大的速率。
在进行模拟/数字信号的转换过程中,当采样频率fs.max大于信号中最高频率Fmax(指低通的,带通的或者高通的有其他的转换方式)的2倍时,即:fs.max>=2Fmax,则采样之后的数字信号完整地保留了原始信号中的信息,就是可以不失真的恢复出原始的模拟信号。一般实际应用中保证采样频率为信号最高频率的5~10倍;采样定理又称奈奎斯特抽样定理。
1924年奈奎斯特(Nyquist)就推导出在理想低通信道的最高大码元传输速率的公式:
理想低通信道的最高大码元传输速率RB=2B(其中B是理想低通信道的带宽)
解释下码元速率,信息速率。
码元速率RB即单位时间里传送的码元个数。单位(Baud)
信息速率Rb是指单位时间里传送的信息量。单位(bit/s,或bPS)
多进制的码元速率和信息速率的关系Rb=RB*log2N(N为进制数,二进制是N为2,就是只能表示两个电平,高和低)。可以看出,对于二进制的信号,码元速率和信息速率在数值上是相等的。
(2)奈奎斯特准则
1924年,奈奎斯特(Nyquist)就推导出在理想低通信道下的最高码元传输速率的公式:
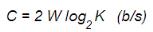
其中W是理想低通信道的带宽,单位为赫兹;K是多相调制的相数。奈氏准则的另一种表达方法是:每赫兹带宽的理想低通信道的最高码元传输速率是每秒2个码元。若码元的传输速率超过了奈氏准则所给出的数值,则将出现码元之间的互相干扰,以致在接收端就无法正确判定码元是1还是0。对于具有理想带通矩形特性的信道(带宽为W),奈氏准则就变为:理想带通信道的最高码元传输速率=1WBaud,即每赫宽带的带通信道的最高码元传输速率为每秒1个码元。奈氏准则是在理想条件下推导出的。在实际条件下,最高码元传输速率要比理想条件下得出的数值还要小些。电信技术人员的任务就是要在实际条件下,寻找出较好的传输码元波形,将比特转换为较为合适的传输信号。
需要注意的是,奈氏准则并没有对信息传输速率(b/s)给出限制。要提高信息传输速率就必须使每一个传输的码元能够代表许多个比特的信息。这就需要有很好的编码技术。
根据奈奎斯特准则我们可以推断出:
(1)给定了信道的带宽,则该信道的极限波特率就确定了,不可能超过这个极限波特率传输码元,除非改善该信道的带宽;
(2)要想增加信道的比特传送率有两条途径,一方面可以增加该信道的带宽,另一方面可以选择更高的编码方式。
例1:例:假设一个传四进制数据信号的无噪声数字信道,带宽为3000Hz,求其信道容量。
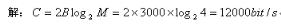
(3)释疑:为什么“当噪声趋于0时,信道容量趋于无限”,适用于香农定律,却不适用于奈奎斯特准则?
附:术语表
Ø信噪比
如果我们在人声嘈杂的集市上向远处的一个人喊话,我们必定会提高自己的声音的音量。我们所喊的话叫做信号,周围环境的声音是噪声。我们的声音越大(信号的功率越大),周围环境越安静则噪声越小(噪声的功率越小),对方就听得越清楚。这说明信号和噪声的功率比越大,越有利于信号的接收。信号和噪声的功率比就叫做信噪比,用S/N表示,单位没有量纲。由于信噪比有时数值很大,在一个通信线路的各个环节里面还要用它进行计算,所以经常对它取常用对数,再乘以10。所得的结果也叫做信噪比,不过这时的单位为分贝(db)。
Ø电平
系统中某点的电平,是指该点的功率P(或电压U)对某一基准功率P0(或基准电压U0)的分贝比。也就是说,“电平”就是指电路中两点或几点在相同阻抗下电量的相对比值。这里的电量自然指“电功率”、“电压”、“电流”并将倍数化为对数,用“分贝”表示,记作“dB”。简单地说,电平就是两个电压或功率的比值的对数形式,例如:两个功率P1和P2的数量比为10000倍,那么它们用对数表示的“分贝比”为:
10lg(P1/P2)=10lg10000=40(dB)
因为功率P和电压U之间有如下的关系:P=U2/Z。所以功率P1/P2的分贝比,可按下式变换成电压U1/U2的分贝比:
10lg(P1/P2)=10lg(U12/Z1)/(U22/Z2)=10lg(U12Z2/U22Z1)
=10lg(U12/U22)=10lg(U1/U2)2=20lg(U1/U2)
即:10lg(P/P0)=20lg(U/U0)
所以,用功率比表示时,前面乘的系数是10;用电压比表示时,前面乘的系数是20。
当基准单位P0为1w时,对应的电平为10lg(P/Iw),单位记为“分贝瓦dBw”;
当基准单位P0为1mw时,对应的电平为10lg(P/Imw),单位记为“分贝毫瓦dBmw”;通常将“分贝毫瓦”简写为“dBm”;
当基准单位U0为1mv时,对应的电平为20lg(U/Imv),单位记为“分贝毫伏dBmv”;
当基准单位U0为1μv时,对应的电平为20lg(U/Iv),单位记为“分贝微伏dBμv”,通常将“分贝微伏”简写为“dB”。
Ø波特率
波特率(也称信息传送速率、码元速率、符号速率、或传码率),其定义为每秒钟传送码元的数目,码元速率的单位为“波特”,常用符号“Baud”表示,简写为“B”。
一个数字脉冲就是一个码元,我们用码元速率表示单位时间内信号波形的变换次数,即单位时间内通过信道传输的码元个数。若信号码元宽度为T秒,则码元速率B为:
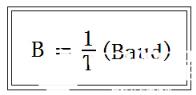
Ø比特率
比特率也称数据传输速率,它的定义是单位时间内可以传输的比特数,单位为bPS。比特率的计算公式为:


香农定理给出了信道信息传送速率的上限(比特每秒)和信道信噪比及带宽的关系。香农定理可以解释现代各种无线制式由于带宽不同,所支持的单载波最大吞吐量的不同。
更多详细内容尽在编程学习网哦!






