Hello大家好,今年数学建模国赛将于9月中旬举行,是时候提前做一些准备了。
本次模型非常简单,只是介绍比较得详细,我下次注意,争取限制下字数。
文末准备了 层次分析-python 模型的实现,简单懂得模型原理便能一眼看懂代码。
文章目录
层次分析(The analytic hierarchy process) 简称AHP,是建模比赛中最基础的模型之一,其主要用于解决评价类问题(例如:选择哪种方案最好、哪位运动员或者员工表现的更优秀等。)
该方法仍具有较强的主观性,判断/比较矩阵的构造在一定程度上是凭感觉决定的,一致性检验只是检验 感觉 有没有自相矛盾得太离谱。
引例:
高考结束,坤坤面临选择大学的问题,摆在他面前的选择有两个:大学A和大学B。
坤坤觉得,他最关心的有四个方面:学习氛围,就业前景,男女比例,校园景色,权重分别为0.4,0.3,0.2,0.1。
那么坤坤要完成的,就是通过调查这两所学校的上面4个特征指标,对其进行打分,完成下表:
| 权重 | 大学A | 大学B | |
| 学习氛围 | 0.4 | ||
| 就业前景 | 0.3 | ||
| 男女比例 | 0.2 | ||
| 校园景色 | 0.1 |
最终,经过坤坤百度以及各种调查,打分如下(要求同一特征不同大学分数之和为1):
| 权重 | 大学A | 大学B | |
| 学习氛围 | 0.4 | 0.6 | 0.4 |
| 就业前景 | 0.3 | 0.5 | 0.5 |
| 男女比例 | 0.2 | 0.3 | 0.7 |
| 校园景色 | 0.1 | 0.2 | 0.8 |
经计算:
- A = 0.4*0.6 + 0.3*0.5 + 0.2*0.3 + 0.1*0.2=0.47
- B = 0.53
B>A 因此最终小坤去了大学B。
即打分法解决评价问题时,只需要我们补充完成下面这张表格即可:
| 权重 | 方案1 | 方案2 | |
| 指标1 | |||
| 指标2 | |||
| 指标3 | |||
| 指标4 |
同颜色单元格之和为1。
题目:
选择好大学后,坤坤准备在开学前去旅游,他决定在城市A,城市B,城市C中选择一个作为目标地点。
请你确定评价指标、形成评价体系来为坤坤同学选择最佳的方案。
从上面居中的这段话中,很直接得就告诉我们这是一个评价类问题,那么我们不妨用刚刚学到的层次分析来解决这个问题。
解决评价类问题,大家首先要想到以下三个问题:
- 我们评价的目标是什么?
- 最佳旅游目标的选择
- 我们为了达到这个目标有哪几种可选的方案?
- 城市A、B、C
- 评价的准则或者说指标是什么?
- 我们根据什么东西来评价好坏?
那么问题来了,对于第三个问题,题目没给相关数据支撑,比如哪里的空气好啊费用低呀... 需要我们查阅相关的资料。
一般而言,前两个问题的答案很容易得到,第三个问题的答案需要我们根据题目中的背景材料、常识以及网上搜集到的参考资料进行结合,从中筛选出最合适的指标。
这个时候,我们就可以去知网(或者万方、百度学术、谷歌学术等平台)搜索相关的文献,这样一来,我们的论文也就有文献引用了,让我们的数据等看起来有理有据,显得专业,还能明目张胆地借鉴学习一下他们论文中的观点。
推荐一个据说很厉害的网站:虫部落快搜 - 搜索快人一步
那么现在,假如我们替坤坤查询了资料后选择了以下五个指标:
- 景点景色
- 旅游花费
- 居住环境
- 饮食情况
- 交通便利程度
接下来,要对坤坤如何提问才能帮他做出合理的决定?
这就要用到我们最开始学的那张表了
| 权重 | 城市A | 城市B | 城市C | |
| 景色 | ||||
| 花费 | ||||
| 居住 | ||||
| 饮食 | ||||
| 交通 |
但是,如果我们直接问坤坤:权重多少,城市ABC评分多少,会显得十分片面且不周全(第二天再问他绝对又换了个数,他自己也记不清。)
在确定影响某因素的诸因子在该因素中所占的比重时,遇到的主要困难 是这些比重常常不易定量化。此外,当影响某因素的因子较多时,直接 考虑各因子对该因素有多大程度的影响时,常常会因考虑不周全、顾此 失彼而使决策者提出与他实际认为的重要性程度不相一致的数据,甚至 有可能提出一组隐含矛盾的数据。
——选自司守奎[kuí]老师的《数学建模算法与应用》
因此,我们采用分而治之的思想,先来处理权重吧~
问题:
- 一次性考虑这五个指标之间的关系,往往考虑不周。
解决方法:
- 两个两个指标进行比较,最终根据两两比较的结果来推算出权重。
1.1 两两比较获得判断矩阵
简单来说就是我们这5个指标分别比较,比如我觉得:景色比花费更重要,饮食比交通非常重要... 通过这样的方式对不同的重要程度赋值 并 最后计算,从而得到权值。
| 标度 | 含义 |
| 1 | 表示两个因素相比,具有同样重要性 |
| 3 | 表示两个因素相比,一个因素比另一个因素稍微重要 |
| 5 | 表示两个因素相比,一个因素比另一个因素明显重要 |
| 7 | 表示两个因素相比,一个因素比另一个因素强烈重要 |
| 9 | 表示两个因素相比,一个因素比另一个因素极端重要 |
| 2,4,6,8 | 上述两相邻判断的中值如2是1和3之间 |
| 倒数 | A和B相比如果标度为3,那么B和A相比就是1/3 |
接下来,就是两两比较五个指标对于选择最终的旅游景点的重要性。
我们绘制如下表格,其对角线肯定都为1:
| 景色 | 花费 | 居住 | 饮食 | 交通 | |
| 景色 | 1 | ||||
| 花费 | 1 | ||||
| 居住 | 1 | ||||
| 饮食 | 1 | ||||
| 交通 | 1 |
问:景色和花费相比的重要程度?
坤:我认为景色比花费略重要,介于同等重要1和稍微重要3之间吧。
问:景色和居住相比的重要程度?
坤: 我认为景色比居住要重要一点,介于稍微重要3和明显重要5之间吧。
| 景色 | 花费 | 居住 | 饮食 | 交通 | |
| 景色 | 1 | 2 | 4 | ||
| 花费 | 1/2 | 1 | |||
| 居住 | 1/4 | 1 | |||
| 饮食 | 1 | ||||
| 交通 | 1 |
这样坤坤回答完10次( ),填完了这张用于计算权重的表格(重要性更加稳定精确了):
| 景色 | 花费 | 居住 | 饮食 | 交通 | |
| 景色 | 1 | 2 | 4 | 3 | 3 |
| 花费 | 2 | 1 | 7 | 5 | 5 |
| 居住 | 1/4 | 1/7 | 1 | 1/2 | 1/3 |
| 饮食 | 1/3 | 1/5 | 2 | 1 | 1 |
| 交通 | 1/3 | 1/5 | 3 | 1 | 1 |
注:实际情况下没有坤坤帮我们回答,层次分析法中这张表是交给‘专家’ 填的,具体我们等后面再说。(其实我们自己凭感觉填,在论文中不说怎么来的也行,后面会有获奖案例鉴赏。)
这样,我们所形成的正互反矩阵,就是层次分析法中的判断矩阵。
得到判断矩阵,我们就可以计算出权重了,方法后面再讲。
同理,我们可以得到城市A、B、C在景色、花费、居住、饮食、交通所占的权重(得分),因此需要再填5张表格,如问完了坤坤对于城市ABC中景色的看法:
| 景色 | 城市A | 城市B | 城市C |
| 城市A | 1 | 2 | 5 |
| 城市B | 1/2 | 1 | 2 |
| 城市C | 1/5 | 1/2 | 1 |
其它关于花费、居住、饮食、交通的表我就略了。
注:一个可能出现问题的地方:
坤坤:我觉得x比y好,y比z好,z比x好或一样好。

如果把语气加重一些,谁比谁非常好,那么这种不一致的现象会更加严重。
1.2 一致性正互反矩阵的引入
此时,我们就要介绍一个东西:一致矩阵,用它来判断数据知否合理。
- 若矩阵中每个元素
且满足
,则我们称该矩阵为正互反矩阵。
- 在层次分析法中,我们构造的判断矩阵均是正互反矩阵。
- 若正互反矩阵满足
,则我们称其为一致矩阵。
| 1 | 2 | 4 |
| 1/2 | 1 | 2 |
| 1/4 | 1/2 | 1 |
你看,上面这个矩阵就是一致矩阵。
比如我让i=1, j=2, k=3, 那么2*2=4:
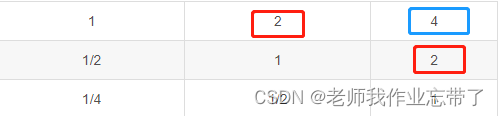
令i=2, j=2, k=1, 那么1*1/2=1/2:
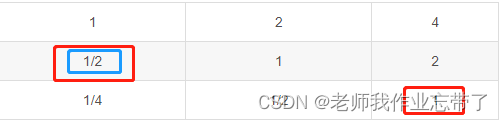
此外除了 一致矩阵还有个特点,就是行或列对应成比例。
我们引入一致矩阵,用来检验我们构造的判断矩阵和一致矩阵是否有太大的差别。
| 景色(原始) | 城市A | 城市B | 城市C |
| 城市A | 1 | 2 | 5 |
| 城市B | 1/2 | 1 | 2 |
| 城市C | 1/5 | 1/2 | 1 |
| 景色(一致矩阵) | 城市A | 城市B | 城市C |
| 城市A | 1 | 2 | 4 |
| 城市B | 1/2 | 1 | 2 |
| 城市C | 1/4 | 1/2 | 1 |
引理:n阶正反矩阵A为一致矩阵时当且仅当最大特征是
;
且当正反矩阵A非一致时,
| 景色 | 城市A | 城市B | 城市C |
| 城市A | 1 | 2 | a |
| 城市B | 1/2 | 1 | 2 |
| 城市C | 1/a | 1/2 | 1 |
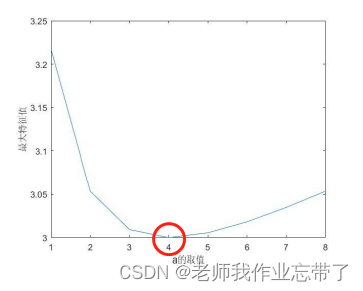
从上图我们可以发现,当a=4也就是上方刚开始介绍的一致矩阵,此时最大特征值最小,为3=n也就是矩阵的阶数。若a不为4,或a离4越来越远,不一致现象越明显,则其特征值也递增。
1.2.1 一致性检验的步骤
计算一致性指标CI
查下表找对应的平均随机一致性指标RI
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| R | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 | 1.46 | 1.49 | 1.52 | 1.54 | 1.56 | 1.58 | 1.59 |
注:在实际运用中,n很少超过10,如果指标的个数大于10,则可考虑建立 二级指标体系,或使用我们以后要学习的模糊综合评价模型。
计算一致性比例CR
如果CR < 0.1, 则可认为判断矩阵的一致性可以接受;
否则需要对判断矩阵进行修正。
1.3 根据一致性正互反矩阵计算权重
以下表为例,虽然不是一致矩阵,但它的CR<0.1,我们选择接受不做调整。
(CR>0.1如何调整在后面)。
| 景色 | 城市A | 城市B | 城市C |
| 城市A | 1 | 2 | 5 |
| 城市B | 1/2 | 1 | 2 |
| 城市C | 1/5 | 1/2 | 1 |
我们取出第一列,做归一化处理(城市ABC对于城市A的重要性是1、1/2、1/4)。
- 城市A = 1 /(1+0.5+0.2) = 0.5882
- 城市B = 0.5/(1+0.5+0.2) = 0.2941
- 城市C = 0.2/(1+0.5+0.2) = 0.1177
之后我们拿出二三列重复上面操作:
- 城市A = 2 /(2+1+0.5) = 0.5714
- 城市B = 1/(2+1+0.5) = 0.2857
- 城市C = 0.5/(2+1+0.5) = = 0.1429
- 城市A = 5 /(5+2+1) = 0.625
- 城市B = 2/(5+2+1) = 0.25
- 城市C = 1/(5+2+1) = 0.125
这样我们得到三组权重:
法1:算术平均求权重:
- 第一步:将判断矩阵按照列归一化 (每一个元素除以其所在列的和)
- 第二步:将归一化的各列相加(按行求和)
- 第三步:将相加后得到的向量中每个元素除以n即可得到权重向量
- 城市A = (0.5882+0.5714+0.625)/3=0.5949
- 城市B = (0.2941+0.2857+0.25)/3=0.2766
- 城市C = (0.1177+0.1429+0.125)/3=0.1285
法2:几何平均法求权重
- 第一步:将A的元素按照行相乘得到一个新的列向量
- 第二步:将新的向量的每个分量开n次方
- 第三步:对该列向量进行归一化即可得到权重向量
- 城市A = 0.5954
- 城市B = 0.2764
- 城市C = 0.1283
法3:特征值法求权重
假如我们的判断矩阵一致性可以接受,那么我们可以仿照一致矩阵权重的求法。
一致矩阵有一个特征值为n,其余特征值均为0。
- 第一步:求出矩阵A的最大特征值以及其对应的特征向量
- 第二步:对求出的特征向量进行归一化即可得到我们的权重
| 景色 | 城市A | 城市B | 城市C |
| 城市A | 1 | 2 | 5 |
| 城市B | 1/2 | 1 | 2 |
| 城市C | 1/5 | 1/2 | 1 |
该表最大特征值为3.0055,一致性比例CR=0.0053,对应的特征向量:[-0.8902,-0.4132,-0.1918],对其进行归一化:[0.5954,0.2764,0.1283]
| 算术平均法 | 几何平均法 | 特征值法 | |
| 城市A | 0.5949 | 0.5954 | 0.5954 |
| 城市B | 0.2766 | 0.2764 | 0.2764 |
| 城市C | 0.1285 | 0.1283 | 0.1283 |
我们大多数情况下使用特征值法,将其带入初始要填的表:
| 权重 | 城市A | 城市B | 城市C | |
| 景色 | 0.5954 | 0.2764 | 0.1283 | |
| 花费 | ||||
| 居住 | ||||
| 饮食 | ||||
| 交通 |
同理这些空着的地方都可以使用同样的方式。
此时,我们终于得到了这个判断矩阵:
| 权重 | 城市A | 城市B | 城市C | |
| 景色 | 0.2636 | 0.5954 | 0.2764 | 0.1283 |
| 花费 | 0.4758 | 0.0819 | 0.2363 | 0.6817 |
| 居住 | 0.0538 | 0.4286 | 0.4286 | 0.1429 |
| 饮食 | 0.0981 | 0.6337 | 0.1919 | 0.1744 |
| 交通 | 0.1087 | 0.1667 | 0.1667 | 0.6667 |
城市A最终得分:0.299
城市B最终得分:0.245
城市C最终得分:0.455
所以最后去城市C旅游。
层次分析法(The Analytic Hierarchy Process即 AHP)是由美国运筹学家、 匹兹堡大学教授T . L. Saaty于20世纪70年代创立的一种系统分析与决策的综合 评价方法,是在充分研究了人类思维过程的基础上提出来的,它较合理地解 决了定性问题定量化的处理过程。
AHP的主要特点是通过建立递阶层次结构,把人类的判断转化到若干因 素两两之间重要度的比较上,从而把难于量化的定性判断转化为可操作的重 要度的比较上面。在许多情况下,决策者可以直接使用AHP进行决策,极大 地提高了决策的有效性、可靠性和可行性,但其本质是一种思维方式,它把 复杂问题分解成多个组成因素,又将这些因素按支配关系分别形成递阶层次 结构,通过两两比较的方法确定决策方案相对重要度的总排序。整个过程体 现了人类决策思维的基本特征,即分解、判断、综合,克服了其他方法回避 决策者主观判断的缺点
步骤:
1.分析系统中各因素之间的关系,建立系统的递阶层次结构.

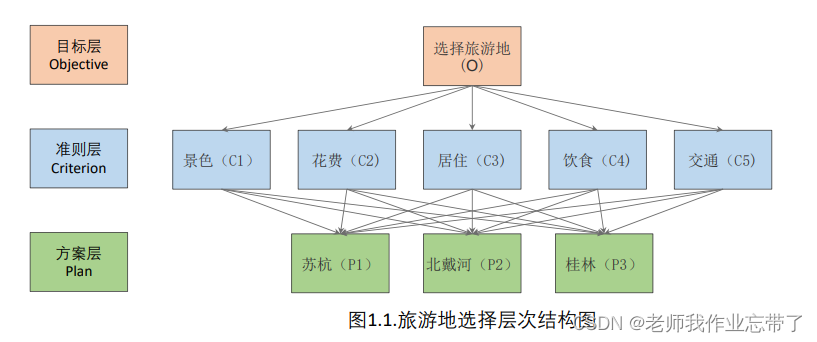
注意:如果你用到了层次分析法,那么上面这个层次结构图要放在你的建模论文中哦。
2. 对于同一层次的各元素关于上一层次中某一准则的重要 性进行两两比较,构造两两比较矩阵(判断矩阵)。
看看优秀论文的做法吧:
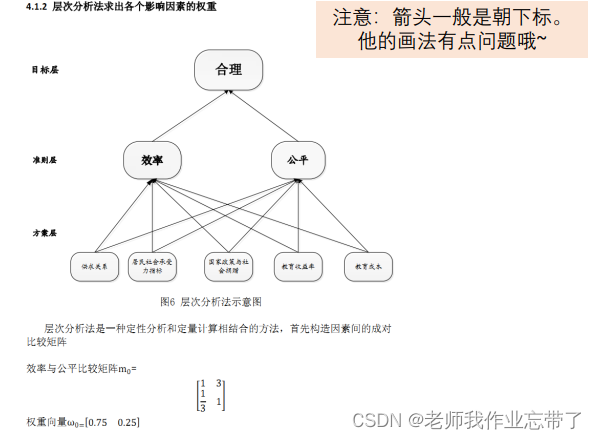
【2008年国赛B题一等奖】 关于高等教育学费标准的评价及建议
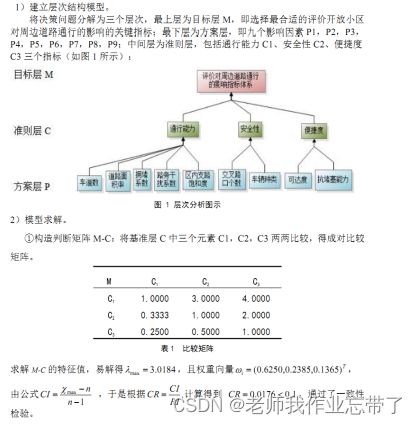
【2016年国赛MATLAB创新奖B题】中国人民大学‐小区开放道路通行影响
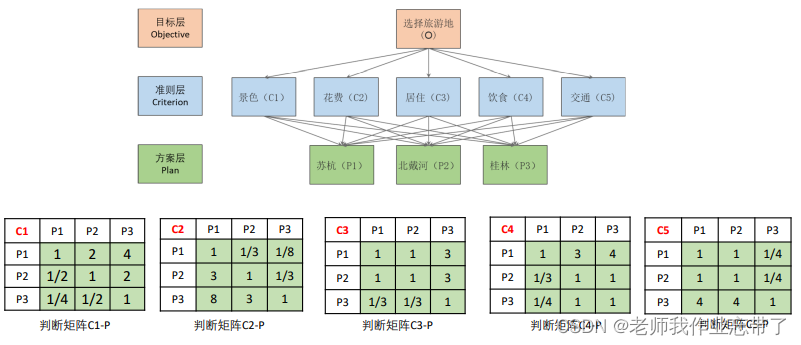
准则层—方案层的判断矩阵的数值要结合实际来填写,如果题目中有其他数据, 可以考虑利用这些数据进行计算。
例如:有一个指标是交通安全程度,现在要比较开放小区、半开放小区和封闭小区,而且 你收集到了这些小区车流量的数据,那么就可以根据这个数据进行换算作为你的判断矩阵。
3. 由判断矩阵计算被比较元素对于该准则的相对权重, 并进行一致性检验(检验通过权重才能用)
CR<0.1通过后,三种3方法计算权重:算术平均、几何平均、特征值法。
建议大家在比赛时三种方法都使用
以往的论文利用层次分析法解决实际问题时,都是采用其中某一种方法求权重,而不同的计算方法可能会导致结果有所偏差。为了保证结果的稳健性,本文采用了三种方法分别求出了权重后计算平均值,再根据得 到的权重矩阵计算各方案的得分,并进行排序和综合分析,这样避免了 采用单一方法所产生的偏差,得出的结论将更全面、更有效。
注:
- 一致矩阵不需要进行一致性检验,只有非一致矩阵的判断矩阵才需要进 行一致性检验;
- 在论文写作中,应该先进行一致性检验,通过检验后再计算 权重,视频中讲解的只是为了顺应计算过程

当CR>0.1时如何修正?
| 指标X | 城市A | 城市B | 城市C |
| 城市A | 1 | 2 | 1 |
| 城市B | 1/2 | 1 | 2 |
| 城市C | 1 | 1/2 | 1 |
答:往一致矩阵上调整,一致矩阵的行列成倍数关系
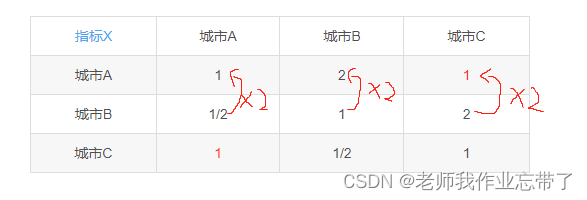
所以:
| 指标X | 城市A | 城市B | 城市C |
| 城市A | 1 | 2 | 4 |
| 城市B | 1/2 | 1 | 2 |
| 城市C | 1/4 | 1/2 | 1 |
根据权重矩阵计算最终得分,并进行排序。
评价的决策层不能太多,太多的话n会很大,判断矩阵和 一致矩阵差异 可能会很大。
我们上面提到过的RI指标也只到了15:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| R | 0 | 0 | 0.52 | 0.89 | 1.12 | 1.26 | 1.36 | 1.41 | 1.46 | 1.49 | 1.52 | 1.54 | 1.56 | 1.58 | 1.59 |
如果决策层中指标的数据是已知的,那么我们如何利用这些数据来使得评价的更加准确呢?
层次分析法中,实际情况下没有坤坤帮我们回答,层次分析法中这张表是交给‘专家’ 填的。(谁比谁重要啊,重要程度是几呀... ),其实我们自己凭感觉填(两两比较的结果)。
该方法仍具有较强的主观性,判断/比较矩阵的构造在一定程度上是凭感觉决定的,一致性检验只是检验 感觉 有没有自相矛盾得太离谱。
1. 多个准则层:
与之前做法一样,不过是多算几组表格。
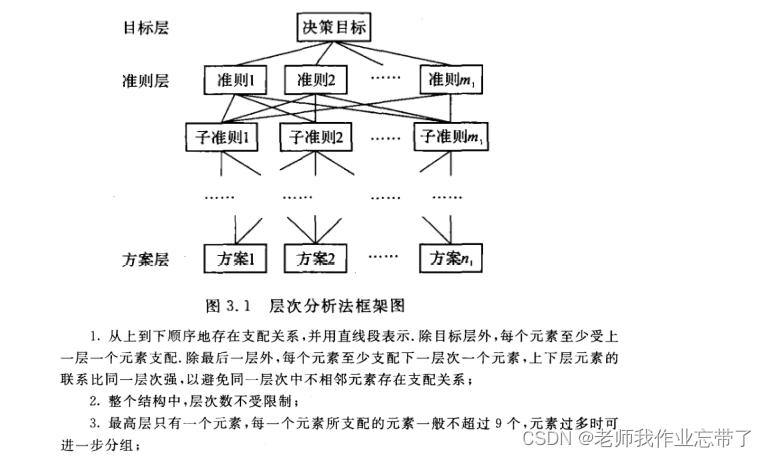
2. 准则不对应全部方案:
可以把另一个方案的权重设为0
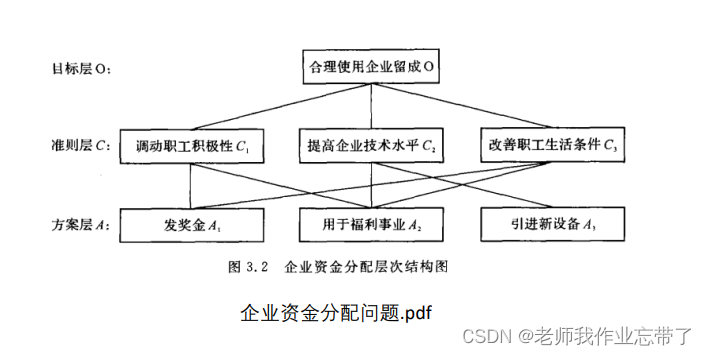
*3. 一个准则只对应自己的方案
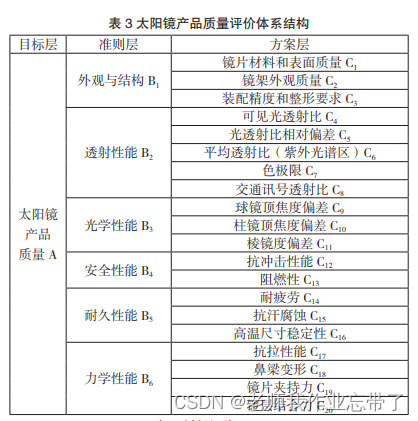
我们只要生成这样的表即可:
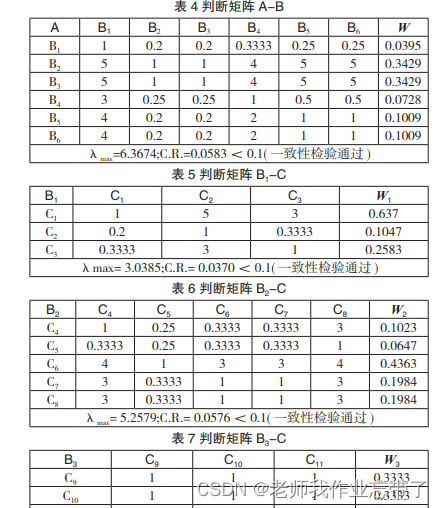
先成大的部分的判断矩阵,再分别处理小的。
感觉这个模型还是很简单的。如果有不理解的地方可以联系帅气的博主。
你要购买一台笔记本电脑,要考虑其:颜值、性能、口碑、重量、保险情况,这5个方面,最终筛选出了3种品牌的电脑。
第一步:
确定了目标层、准则层、方案层后,我们要做的就是填下表:
| 权重 | 电脑A | 电脑B | 电脑C | |
| 颜值 | ||||
| 性能 | ||||
| 口碑 | ||||
| 重量 | ||||
| 保险情况 |
第二步:
我们先处理第一列(权重),其判断矩阵如下。
| 颜值 | 性能 | 口碑 | 重量 | 保险情况 | |
| 颜值 | 1 | 1/2 | 4 | 3 | 3 |
| 性能 | 2 | 1 | 7 | 5 | 5 |
| 口碑 | 1/4 | 1/7 | 1 | 1/2 | 1/3 |
| 重量 | 1/3 | 1/5 | 2 | 1 | 1 |
| 保险情况 | 1/3 | 1/5 | 3 | 1 | 1 |
matrix = np.array([[1, 1 / 2, 4, 3, 3], [2, 1, 7, 5, 5], [1 / 4, 1 / 7, 1, 1 / 2, 1 / 3], [1 / 3, 1 / 5, 2, 1, 1],
[1 / 3, 1 / 5, 3, 1, 1]])
下面我就以上面这个判断矩阵为例子,定义权重类:
代码1:
- 只定义了权重求解类,初始化时要传入一个判断矩阵。
- 往往我们层次分析问题要求解多个判断矩阵,可以自己在这基础之上定义一个AHP类,初始化时把全部判断矩阵都放进去,直接内部计算输出选择方案。
import numpy as np# 计算权重类# 首先初始化判断矩阵,检验其CR是否<0.1,如果小于则计算权重,否则提示调整矩阵内数值。class Calculate_weights: # 初始化判断矩阵 def __init__(self, array): self.array = array # n为矩阵维度 self.n = array.shape[0] # 矩阵的特征值和特征向量 self.eig_val, self.eig_vector = np.linalg.eig(self.array) # 矩阵的最大特征值 self.max_eig_val = np.max(self.eig_val) # 矩阵最大特征值对应的特征向量 self.max_eig_vector = self.eig_vector[:, np.argmax(self.eig_val)].real # 矩阵的一致性指标CI self.CI_value = (self.max_eig_val - self.n) / (self.n - 1) # 平均随机一致性指标RI值列表,用于一致性检验。 self.RI_list = [0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58, 1.59] # 矩阵的一致性比例CR self.CR_value = self.CI_value / (self.RI_list[self.n - 1]) # 一致性判断 返回布尔类型 def test_consist(self): # 打印矩阵的一致性指标CI和一致性比例CR # 进行一致性检验判断 if self.n == 2 or self.CR_value < 0.1: # 二阶矩阵或CR值小于0.1,可以通过一致性检验。 return True else: # CR值大于0.1, 一致性检验不通过。 print("判断矩阵的CR值为:" + str(self.CR_value) + ",未通过一致性检验。") return False # 算术平均法求权重 def cal_weight_by_arithmetic_method(self): # 求矩阵的每列的和 col_sum = np.sum(self.array, axis=0) # 将判断矩阵按照列归一化 array_normed = self.array / col_sum # 计算权重向量 array_weight = np.sum(array_normed, axis=1) / self.n # 打印权重向量 print("算术平均法计算得到的权重为:\n", array_weight) # 返回权重向量的值 return array_weight # 几何平均法求权重 def cal_weight_by_geometric_method(self): # 求矩阵的每列的积 col_product = np.product(self.array, axis=1) # 将得到的积向量的每个分量进行开n次方 array_power = np.power(col_product, 1 / self.n) # 将列向量归一化 array_weight = array_power / np.sum(array_power) # 打印权重向量 print("几何平均法计算得到的权重为:\n", array_weight) # 返回权重向量的值 return array_weight # 特征值法求权重 def cal_weight_by_eigenvalue_method(self): # 将矩阵最大特征值对应的特征向量进行归一化处理就得到了权重 array_weight = self.max_eig_vector / np.sum(self.max_eig_vector) # 打印权重向量 print("特征值法计算得到的权重为:\n", array_weight) # 返回权重向量的值 return array_weightif __name__ == "__main__": # 给出判断矩阵 matrix = np.array([[1, 1 / 2, 4, 3, 3], [2, 1, 7, 5, 5], [1 / 4, 1 / 7, 1, 1 / 2, 1 / 3], [1 / 3, 1 / 5, 2, 1, 1], [1 / 3, 1 / 5, 3, 1, 1]]) # 权重对象 weights_obj = Calculate_weights(matrix) if weights_obj.test_consist(): # 算术平均法求权重 weight1 = weights_obj.cal_weight_by_arithmetic_method() # 几何平均法求权重 weight2 = weights_obj.cal_weight_by_geometric_method() # 特征值法求权重 weight3 = weights_obj.cal_weight_by_eigenvalue_method()算术平均法计算得到的权重为: [0.26228108 0.47439499 0.0544921 0.09853357 0.11029827]几何平均法计算得到的权重为: [0.2636328 0.47726387 0.05307416 0.09883999 0.10718918]特征值法计算得到的权重为: [0.26360349 0.47583538 0.0538146 0.09806829 0.10867824]
很明显,性能要更重要一些:
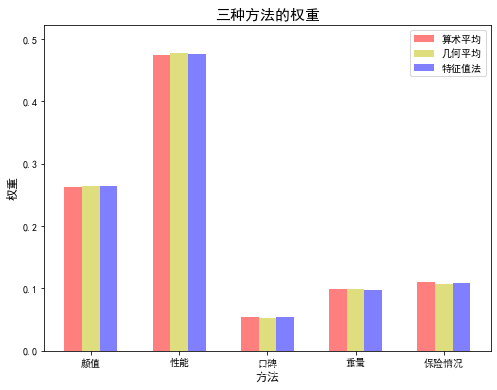
因此我们填完了表的第一列:
| 权重 | 电脑A | 电脑B | 电脑C | |
| 颜值 | 0.2636 | |||
| 性能 | 0.4758 | |||
| 口碑 | 0.0538 | |||
| 重量 | 0.0980 | |||
| 保险情况 | 0.1086 |
其它列同理。
代码2:
- AHP类,初始化时把全部判断矩阵都放进去,直接内部计算输出选择方案。
总之要学会变通。
import numpy as np# 计算权重类# 首先初始化判断矩阵,检验其CR是否<0.1,如果小于则计算权重,否则提示调整矩阵内数值。class Calculate_weights: # 初始化判断矩阵 def __init__(self, array): self.array = array # n为矩阵维度 self.n = array.shape[0] # 矩阵的特征值和特征向量 self.eig_val, self.eig_vector = np.linalg.eig(self.array) # 矩阵的最大特征值 self.max_eig_val = np.max(self.eig_val) # 矩阵最大特征值对应的特征向量 self.max_eig_vector = self.eig_vector[:, np.argmax(self.eig_val)].real # 矩阵的一致性指标CI self.CI_value = (self.max_eig_val - self.n) / (self.n - 1) # 平均随机一致性指标RI值列表,用于一致性检验。 self.RI_list = [0, 0, 0.52, 0.89, 1.12, 1.26, 1.36, 1.41, 1.46, 1.49, 1.52, 1.54, 1.56, 1.58, 1.59] # 矩阵的一致性比例CR self.CR_value = self.CI_value / (self.RI_list[self.n - 1]) # 一致性判断 返回布尔类型 def test_consist(self): # 打印矩阵的一致性指标CI和一致性比例CR # 进行一致性检验判断 if self.n == 2 or self.CR_value < 0.1: # 二阶矩阵或CR值小于0.1,可以通过一致性检验。 return True else: # CR值大于0.1, 一致性检验不通过。 print("判断矩阵的CR值为:" + str(self.CR_value) + ",未通过一致性检验。") return False # 算术平均法求权重 def cal_weight_by_arithmetic_method(self): # 求矩阵的每列的和 col_sum = np.sum(self.array, axis=0) # 将判断矩阵按照列归一化 array_normed = self.array / col_sum # 计算权重向量 array_weight = np.sum(array_normed, axis=1) / self.n # 打印权重向量 #print("算术平均法计算得到的权重为:\n", array_weight) # 返回权重向量的值 return array_weight # 几何平均法求权重 def cal_weight_by_geometric_method(self): # 求矩阵的每列的积 col_product = np.product(self.array, axis=1) # 将得到的积向量的每个分量进行开n次方 array_power = np.power(col_product, 1 / self.n) # 将列向量归一化 array_weight = array_power / np.sum(array_power) # 打印权重向量 #print("几何平均法计算得到的权重为:\n", array_weight) # 返回权重向量的值 return array_weight # 特征值法求权重 def cal_weight_by_eigenvalue_method(self): # 将矩阵最大特征值对应的特征向量进行归一化处理就得到了权重 array_weight = self.max_eig_vector / np.sum(self.max_eig_vector) # 打印权重向量 #print("特征值法计算得到的权重为:\n", array_weight) # 返回权重向量的值 return array_weightclass AHP: def __init__(self, *args): self.col = args[0] self.row = args[1] self.array = args[2:] # 初始化最终矩阵 self.finally_matrix = np.empty((len(self.row),len(self.col),)) # 生成全部填好后的最终矩阵 def f_matrix(self): # matrix 为每个判断矩阵,记得注意顺序,如权重在第一列。 col = 0 row = 0 for matrix in self.array: weights_obj = Calculate_weights(matrix) if weights_obj.test_consist(): # 特征值法求权重 weight3 = weights_obj.cal_weight_by_eigenvalue_method() if col == 0: # 权重的权重放在列(竖着放在第一列) self.finally_matrix[:, col] = weight3 col += 1 else: # 剩下的都放在行(每行横着放) self.finally_matrix[row, col:] = weight3 row += 1 return self.finally_matrix def result(self): self.f_matrix() res = [] for i in range(len(self.col)-1): tem_res = np.sum(self.finally_matrix[:,0]*self.finally_matrix[:,i+1]) res.append(tem_res) return resif __name__ == "__main__": # 给出判断矩阵 col = ['权重', '电脑A', '电脑B', '电脑C'] row = ['颜值', '性能', '口碑', '重量', '保险'] weighting = np.array( [[1, 1 / 2, 4, 3, 3], [2, 1, 7, 5, 5], [1 / 4, 1 / 7, 1, 1 / 2, 1 / 3], [1 / 3, 1 / 5, 2, 1, 1], [1 / 3, 1 / 5, 3, 1, 1]]) appearance = np.array([[1, 2, 5], [1 / 2, 1, 2], [1 / 5, 1 / 2, 1]]) performance = np.array([[1, 1 / 3, 1 / 8], [3, 1, 1 / 3], [8, 3, 1]]) public_praise = np.array([[1, 1, 3], [1, 1, 3], [1 / 3, 1 / 3, 1]]) weight = np.array([[1, 3, 4], [1 / 3, 1, 1], [1 / 4, 1, 1]]) insurance = np.array([[1, 1, 1 / 4], [1, 1, 1 / 4], [4, 4, 1]]) score_result = AHP(col, row, weighting, appearance, performance, public_praise, weight, insurance).result() print('选择{}'.format(col[np.argmax(score_result)+1])) 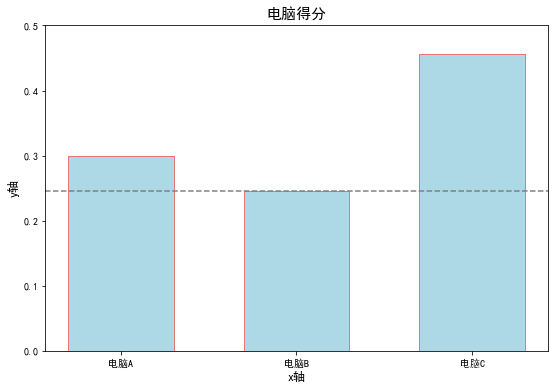
选择电脑C。
来源地址:https://blog.csdn.net/suic009/article/details/126130874






