大家好,今天和各位分享一下 SAC (Soft Actor Critic) 算法,一种基于最大熵的无模型的深度强化学习算法。基于 OpenAI 的 gym 环境完成一个小案例,完整代码可以从我的 GitHub 中获得:
https://github.com/LiSir-HIT/Reinforcement-Learning/tree/main/Model
1. 基本原理
Deepmind 提出的 SAC (Soft Actor Critic) 算法是一种基于最大熵的无模型的深度强化学习算法,适合于真实世界的机器人学习技能。SAC 算法的效率非常高,它解决了离散动作空间和连续性动作空间的强化学习问题。SAC 算法在以最大化未来累积奖励的基础上引入了最大熵的概念,加入熵的目的是增强鲁棒性和智能体的探索能力。SAC 算法的目的是使未来累积奖励值和熵最大化,使得策略尽可能随机,即每个动作输出的概率尽可能的分散,而不是集中在一个动作上。
SAC 算法的目标函数表达式如下:
![J(\pi)=\sum_{t=0}^{T} E_{(s_t,a_t)\sim \rho^\pi} [r(s_t,a_t) + \alpha H(\pi(\cdot | s_t))]](https://file.lsjlt.com/upload/f/202309/03/5uhtchum1ng.png)
其中 T 表示智能体与环境互动的总时间步数,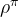 表示在策略
表示在策略 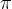 下
下 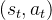 的分布,
的分布, 代表熵值,
代表熵值,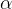 代表超参数,它的目的是控制最优策略的随机程度和权衡熵相对于奖励的重要性。
代表超参数,它的目的是控制最优策略的随机程度和权衡熵相对于奖励的重要性。
2. 公式推导
SAC 是一种基于最大化熵理论的算法。由于目标函数中加入熵值,这使得该算法的探索能力和鲁棒性得到了很大的提升,尽可能的在奖励值和熵值(即策略的随机性)之间取得最大化平衡。智能体因选择动作的随机性(更高的熵)而获得更高的奖励值,以使它不要过早收敛到某个次优确定性策略,即局部最优解。熵值越大,对环境的探索就越多,避免了策略收敛至局部最优,从而可以加快后续的学习速度。
因此,最优策略的 SAC 公式定义为:
![H(\pi (\cdot | s_t)) = E[-log \pi(\cdot | s_t)]](https://file.lsjlt.com/upload/f/202309/03/uhay4fm1ijd.png)
其中 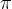 用来更新已找到最大总奖励的策略;
用来更新已找到最大总奖励的策略;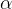 是熵正则化系数,用来控制熵的重要程度;
是熵正则化系数,用来控制熵的重要程度; 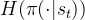 代表熵值,熵值越大,智能体对环境的探索度越大,使智能体能够找到一个更高效的策略,有助于加快后续的策略学习。
代表熵值,熵值越大,智能体对环境的探索度越大,使智能体能够找到一个更高效的策略,有助于加快后续的策略学习。
SAC 的 Q 值可以用基于熵值改进的贝尔曼方差来计算,价值函数定义如下:
![Q(s_t,a_t) = E_{s_{t+1}\sim D} [r(s_t,a_t) + \gamma V^\pi (s_{t+1})]](https://file.lsjlt.com/upload/f/202309/03/aap1vfbjq5a.png)
其中,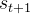 从经验回放池 D 中采样获得,状态价值函数定义如下:
从经验回放池 D 中采样获得,状态价值函数定义如下:
![V(s_t) = E_{a_t\sim \pi} [Q(s_t,a_t) - \alpha log \pi (\cdot | s_t)] = E_{a_t\sim \pi} [Q(s_t,a_t) + H(\pi(\cdot | s_t))]](https://file.lsjlt.com/upload/f/202309/03/spauybym301.png)
它表示在某个状态下预期得到的奖励。此外,SAC 中的策略网络 ,软状态价值网络
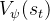 ,目标状态价值网络网络
,目标状态价值网络网络 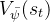 ,以及 2 个软 Q 网络
,以及 2 个软 Q 网络 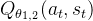 ,它们分别由
,它们分别由 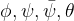 参数化。
参数化。
因此 SAC 中包含 5 个神经网络:策略网络 ,行为价值函数
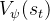 ,目标函数
,目标函数 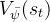 ,行为价值函数
,行为价值函数 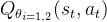 。为了分别找到最优策略,将随机梯度下降法应用于他们的目标函数中。
。为了分别找到最优策略,将随机梯度下降法应用于他们的目标函数中。

此外,还采用了类似于双 Q 网络的形式,软 Q 值的最小值取两个由 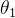 和
和 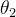 参数化的 Q 值函数,这有助于避免过高估计不恰当的 Q 值,以提高训练速度。软 Q 值函数通过最小化贝尔曼误差来更新:
参数化的 Q 值函数,这有助于避免过高估计不恰当的 Q 值,以提高训练速度。软 Q 值函数通过最小化贝尔曼误差来更新:

策略网络通过最小化 Kullback-Leibler(KL) 散度来更新:

算法流程如下:

3. 代码实现
这里以离散问题为例构建SAC,离线学习,代码如下:
# 处理离散问题的模型import torchfrom torch import nnfrom torch.nn import functional as Fimport numpy as npimport collectionsimport random# ----------------------------------------- ## 经验回放池# ----------------------------------------- #class ReplayBuffer: def __init__(self, capacity): # 经验池容量 self.buffer = collections.deque(maxlen=capacity) # 队列,先进先出 # 经验池增加 def add(self, state, action, reward, next_state, done): self.buffer.append((state, action, reward, next_state, done)) # 随机采样batch组 def sample(self, batch_size): transitions = random.sample(self.buffer, batch_size) # 取出这batch组数据 state, action, reward, next_state, done = zip(*transitions) return np.array(state), action, reward, np.array(next_state), done # 当前时刻的经验池容量 def size(self): return len(self.buffer)# ----------------------------------------- ## 策略网络# ----------------------------------------- #class PolicyNet(nn.Module): def __init__(self, n_states, n_hiddens, n_actions): super(PolicyNet, self).__init__() self.fc1 = nn.Linear(n_states, n_hiddens) self.fc2 = nn.Linear(n_hiddens, n_actions) # 前向传播 def forward(self, x): # 获取当前状态下的动作选择概率 x = self.fc1(x) # [b,n_states]-->[b,n_hiddens] x = F.relu(x) x = self.fc2(x) # [b,n_hiddens]-->[b,n_actions] # 每个状态下对应的每个动作的动作概率 x = F.softmax(x, dim=1) # [b,n_actions] return x# ----------------------------------------- ## 价值网络# ----------------------------------------- #class ValueNet(nn.Module): def __init__(self, n_states, n_hiddens, n_actions): super(ValueNet, self).__init__() self.fc1 = nn.Linear(n_states, n_hiddens) self.fc2 = nn.Linear(n_hiddens, n_actions) # 当前时刻的state_value def forward(self, x): x = self.fc1(x) # [b,n_states]-->[b,n_hiddens] x = F.relu(x) x = self.fc2(x) # [b,n_hiddens]-->[b,n_actions] return x# ----------------------------------------- ## 模型构建# ----------------------------------------- #class SAC: def __init__(self, n_states, n_hiddens, n_actions, actor_lr, critic_lr, alpha_lr, target_entropy, tau, gamma, device): # 实例化策略网络 self.actor = PolicyNet(n_states, n_hiddens, n_actions).to(device) # 实例化第一个价值网络--预测 self.critic_1 = ValueNet(n_states, n_hiddens, n_actions).to(device) # 实例化第二个价值网络--预测 self.critic_2 = ValueNet(n_states, n_hiddens, n_actions).to(device) # 实例化价值网络1--目标 self.target_critic_1 = ValueNet(n_states, n_hiddens, n_actions).to(device) # 实例化价值网络2--目标 self.target_critic_2 = ValueNet(n_states, n_hiddens, n_actions).to(device) # 预测和目标的价值网络的参数初始化一样 self.target_critic_1.load_state_dict(self.critic_1.state_dict()) self.target_critic_2.load_state_dict(self.critic_2.state_dict()) # 策略网络的优化器 self.actor_optimizer = torch.optim.Adam(self.actor.parameters(), lr=actor_lr) # 目标网络的优化器 self.critic_1_optimizer = torch.optim.Adam(self.critic_1.parameters(), lr=critic_lr) self.critic_2_optimizer = torch.optim.Adam(self.critic_2.parameters(), lr=critic_lr) # 初始化可训练参数alpha self.log_alpha = torch.tensor(np.log(0.01), dtype=torch.float) # alpha可以训练求梯度 self.log_alpha.requires_grad = True # 定义alpha的优化器 self.log_alpha_optimizer = torch.optim.Adam([self.log_alpha], lr=alpha_lr) # 属性分配 self.target_entropy = target_entropy self.gamma = gamma self.tau = tau self.device = device # 动作选择 def take_action(self, state): # 输入当前状态 [n_states] # 维度变换 numpy[n_states]-->tensor[1,n_states] state = torch.tensor(state[np.newaxis,:], dtype=torch.float).to(self.device) # 预测当前状态下每个动作的概率 [1,n_actions] probs = self.actor(state) # 构造与输出动作概率相同的概率分布 action_dist = torch.distributions.Categorical(probs) # 从当前概率分布中随机采样tensor-->int action = action_dist.sample().item() return action # 计算目标,当前状态下的state_value def calc_target(self, rewards, next_states, dones): # 策略网络预测下一时刻的state_value [b,n_states]-->[b,n_actions] next_probs = self.actor(next_states) # 对每个动作的概率计算ln [b,n_actions] next_log_probs = torch.log(next_probs + 1e-8) # 计算熵 [b,1] entropy = -torch.sum(next_probs * next_log_probs, dim=1, keepdims=True) # 目标价值网络,下一时刻的state_value [b,n_actions] q1_value = self.target_critic_1(next_states) q2_value = self.target_critic_2(next_states) # 取出最小的q值 [b, 1] min_qvalue = torch.sum(next_probs * torch.min(q1_value,q2_value), dim=1, keepdims=True) # 下个时刻的state_value [b, 1] next_value = min_qvalue + self.log_alpha.exp() * entropy # 时序差分,目标网络输出当前时刻的state_value [b, n_actions] td_target = rewards + self.gamma * next_value * (1-dones) return td_target # 软更新,每次训练更新部分参数 def soft_update(self, net, target_net): # 遍历预测网络和目标网络的参数 for param_target, param in zip(target_net.parameters(), net.parameters()): # 预测网络的参数赋给目标网络 param_target.data.copy_(param_target.data*(1-self.tau) + param.data*self.tau) # 模型训练 def update(self, transition_dict): # 提取数据集 states = torch.tensor(transition_dict['states'], dtype=torch.float).to(self.device) # [b,n_states] actions = torch.tensor(transition_dict['actions']).view(-1,1).to(self.device) # [b,1] rewards = torch.tensor(transition_dict['rewards'], dtype=torch.float).view(-1,1).to(self.device) # [b,1] next_states = torch.tensor(transition_dict['next_states'], dtype=torch.float).to(self.device) # [b,n_states] dones = torch.tensor(transition_dict['dones'], dtype=torch.float).view(-1,1).to(self.device) # [b,1] # --------------------------------- # # 更新2个价值网络 # --------------------------------- # # 目标网络的state_value [b, 1] td_target = self.calc_target(rewards, next_states, dones) # 价值网络1--预测,当前状态下的动作价值 [b, 1] critic_1_qvalues = self.critic_1(states).gather(1, actions) # 均方差损失 预测-目标 critic_1_loss = torch.mean(F.mse_loss(critic_1_qvalues, td_target.detach())) # 价值网络2--预测 critic_2_qvalues = self.critic_2(states).gather(1, actions) # 均方差损失 critic_2_loss = torch.mean(F.mse_loss(critic_2_qvalues, td_target.detach())) # 梯度清0 self.critic_1_optimizer.zero_grad() self.critic_2_optimizer.zero_grad() # 梯度反传 critic_1_loss.backward() critic_2_loss.backward() # 梯度更新 self.critic_1_optimizer.step() self.critic_2_optimizer.step() # --------------------------------- # # 更新策略网络 # --------------------------------- # probs = self.actor(states) # 预测当前时刻的state_value [b,n_actions] log_probs = torch.log(probs + 1e-8) # 小于0 [b,n_actions] # 计算策略网络的熵>0 [b,1] entropy = -torch.sum(probs * log_probs, dim=1, keepdim=True) # 价值网络预测当前时刻的state_value q1_value = self.critic_1(states) # [b,n_actions] q2_value = self.critic_2(states) # 取出价值网络输出的最小的state_value [b,1] min_qvalue = torch.sum(probs * torch.min(q1_value, q2_value), dim=1, keepdim=True) # 策略网络的损失 actor_loss = torch.mean(-self.log_alpha.exp() * entropy - min_qvalue) # 梯度更新 self.actor_optimizer.zero_grad() actor_loss.backward() self.actor_optimizer.step() # --------------------------------- # # 更新可训练遍历alpha # --------------------------------- # alpha_loss = torch.mean((entropy-self.target_entropy).detach() * self.log_alpha.exp()) # 梯度更新 self.log_alpha_optimizer.zero_grad() alpha_loss.backward() self.log_alpha_optimizer.step() # 软更新目标价值网络 self.soft_update(self.critic_1, self.target_critic_1) self.soft_update(self.critic_2, self.target_critic_2)4. 案例演示
基于 OpenAI 的 gym 环境完成一个推车游戏,一个离散的环境,目标是左右移动小车将黄色的杆子保持竖直。动作维度为2,属于离散值;状态维度为 4,分别是坐标、速度、角度、角速度。


训练部分的代码如下:
import gym import torchimport numpy as npimport matplotlib.pyplot as pltfrom RL_brain import ReplayBuffer, SAC# -------------------------------------- ## 参数设置# -------------------------------------- #num_epochs = 100 # 训练回合数capacity = 500 # 经验池容量min_size = 200 # 经验池训练容量batch_size = 64n_hiddens = 64actor_lr = 1e-3 # 策略网络学习率critic_lr = 1e-2 # 价值网络学习率alpha_lr = 1e-2 # 课训练变量的学习率target_entropy = -1tau = 0.005 # 软更新参数gamma = 0.9 # 折扣因子device = torch.device('cuda') if torch.cuda.is_available() \else torch.device('cpu')# -------------------------------------- ## 环境加载# -------------------------------------- #env_name = "CartPole-v1"env = gym.make(env_name, render_mode="human")n_states = env.observation_space.shape[0] # 状态数 4n_actions = env.action_space.n # 动作数 2# -------------------------------------- ## 模型构建# -------------------------------------- #agent = SAC(n_states = n_states, n_hiddens = n_hiddens, n_actions = n_actions, actor_lr = actor_lr, critic_lr = critic_lr, alpha_lr = alpha_lr, target_entropy = target_entropy, tau = tau, gamma = gamma, device = device, )# -------------------------------------- ## 经验回放池# -------------------------------------- #buffer = ReplayBuffer(capacity=capacity)# -------------------------------------- ## 模型构建# -------------------------------------- #return_list = [] # 保存每回合的returnfor i in range(num_epochs): state = env.reset()[0] epochs_return = 0 # 累计每个时刻的reward done = False # 回合结束标志 while not done: # 动作选择 action = agent.take_action(state) # 环境更新 next_state, reward, done, _, _ = env.step(action) # 将数据添加到经验池 buffer.add(state, action, reward, next_state, done) # 状态更新 state = next_state # 累计回合奖励 epochs_return += reward # 经验池超过要求容量,就开始训练 if buffer.size() > min_size: s, a, r, ns, d = buffer.sample(batch_size) # 每次取出batch组数据 # 构造数据集 transition_dict = {'states': s, 'actions': a, 'rewards': r, 'next_states': ns, 'dones': d} # 模型训练 agent.update(transition_dict) # 保存每个回合return return_list.append(epochs_return) # 打印回合信息 print(f'iter:{i}, return:{np.mean(return_list[-10:])}')# -------------------------------------- ## 绘图# -------------------------------------- #plt.plot(return_list)plt.title('return')plt.show()运行100个回合,绘制每个回合的 return





