没有Cocos2D基础?感觉学习Cocos2D很难?多看看编程学习网的教程,让你零基础成游戏开发大神,本篇教程将教你如何怎么用PID控制物理体。
本文将利用某种方法使静止或移动的物体平稳的旋转。我使用Cocos2d-x的Box2D作为物理体,但这个方法在任何物理体上都是通用的(甚至是一个在2D平面上的3D物体)。
这个方法是通过使用比例-积分-微分(PID)控制力矩去使物体角度不断改变。 从视频中可以看到这使用这种方法的两个例子,第一个导弹只能向他面向的方向移动,另一个“实体”则像一个游戏角色一样,他移动的方向与他面向的方向可以是不同的。
面向的方向
无论你的游戏是2D或3D模式,通常你需要“旋转”一个对象使他面朝另一个方向。这可能是一个角色行走移动的方向,蹲坐着射击的方向,导弹飞行的方向,或者是一辆汽车飞驰的方向,等等。这些都是“角色控制器”的工作,你的游戏系统中负责每个角色基本的“运动”(寻找目标地点,转向,移动到达,等等)操作的一系列代码。
使用物理引擎构建游戏有很多的乐趣,在游戏中加入更多真实效果的可以显著改善游戏体验。用更真实的方法去使物体产生碰撞,破裂,旋转,反弹,移动。
但是,实际上的面向一个方向通常与想象中不太一样。你通常关心的是类似于“这个角色需要在0.5秒的时间内向左转。“从物理学的角度来看,这意味着您想应用扭矩,使其在0.5秒内向左旋转90°,然后立即停止。你不想考虑诸如角动量将使它继续旋转,除非你使用反扭矩。不考虑应用反扭矩的原因是他会立即停止。Box2D将允许您手动设置他的的位置和角度。然而,如果你在每一帧都手动设置物体位置和角度的话,(根据我的经验)物理引擎碰撞响应会受到干扰。
最重要的是,这是一个物理引擎。你应该让物体以现实的物理方式移动。我们的目标是应用转动转矩来创建一个解决方案来改变方向问题。注意,PID控制回路可以用于很多其他的东西。这只是我选中的一个例子。
如果我们从问题“如何移动”中分离出一个小问题“如何转向”,我们可以对需要控制的其他类型的移动使用相同的解决方案。对于本文,我们考虑控制正在向其目标移动的导弹。
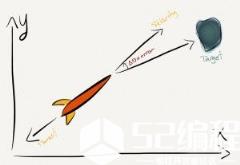
在这里,导弹正朝着一个方向以一个给定的速度移动。速度测量的角度相对于x轴。导弹“面朝的方向”就是鼻头方向而且它只能前进。我们想转动它到另一个角度以便它能够朝向目标。为了使导弹能击中目标,它必须瞄准目标。注意,如果我们谈论的是一个不动的对象,我们很容易的就可以利用对象之间的相对角度与x轴的角度关系求出。
反馈控制系统101
控制系统背后的基本思想是把“你想要的值”和“真实值是什么”,输入到系统中进行调整,这样,随着时间的推移,系统趋向得到你想要的值。
维基百科有文章解释了:
控制回路的一个熟悉的例子是调整冷热龙头(阀门)水保持所需的温度时。这一般涉及两个过程的混合流入,热水和冷水。人接触到水的感觉或测量其温度。基于此反馈执行控制操作调整热水和冷水阀大小,直到温度稳定在所需的值。
控制系统理论有很多知识。多项式,极点,零点,时间域,频率域,状态矢量空间等。无论你有没有学过这方面的东西,它看起来都是很深奥的!也就是说,虽然有更多的“先进”的方法来控制方向,但我们将坚持使用PID来控制。PID控制有明显优势,就是只需“调整”三个参数就能直观的“感受”它的变化。
PID控制
让我们从想“控制”的最基本的变量开始,即角度,认识我们要得到的方向和当前角度之间角度的差异关系:
e(t)=desired-actual
e(t)=期望值-实际值
在这里,e(t)是“差值”。我们想把差值变成0。我们给物体添加一个力,使其不断旋转改变方向,让e(t)趋向0。为此,我们创建一个函数f(.),以e(t)为变量,并在这个基础上为物体添加转矩。转矩使物体旋转:
torque(t)=I*f(e(t)),I≡AngularInertia
torque(t)=I*f(e(t)),I恒等于转动惯性
比例反馈
第一个也是最显而易见的选择是转矩与e(t)本身成正比。当差值越大,受到的力越大。当差值越小,作用力越小。公式如下 :
f(e(t))=Kp*e(t),Kp是系数
应用扭矩能用来作为平衡反馈。但有个问题是,差值越小,纠正扭矩越小。这样当物体的e(t)足够小(接近预期角度),制动转矩也变得很小。所以物体会旋转超过目标角度。然后开始回摆,最终来回摇摆。如果该值Kp不是太大,摇摆会呈现“阻尼”(指数衰减)的正弦曲线,每次摇摆数值下降较快(稳定的解)。数值会螺旋下降到无穷小(不稳定的解),或者只是在目标点不停摆动(稍微稳定的解)。但如果你减少Kp,它就不能较快的改变,当e(t)很大,你将没有足够动力去改变角度。
纯粹比例差值也会出现偏差(稳态误差),使最终的输出与输入的不同。下面公式是Kp函数的差值:
SteadyStateError=desired[1+constant*Kp]
稳态差值=desired[1+常数*Kp]
所以增加Kp值会减少偏差(利)。但这也会使其摇摆(弊)。
积分反馈
下面添加积分项,即PID中的的“I”:
f(e(t))=Kp*e(t)+∫-∞nowKi*e(t)
对于每一个时间间隔来说,如果e(t)是一个固定值,积分项就能计算出来这些:
如果目标方向突然改变一点点,然后在每个时间间隔,这种差异将呈现出来并建立新的扭矩值。
如果方向存在偏差(例如稳态差值),每个时间间隔差值都会累积增加并被计算出来。
积分项可以用来抵消输出时的常值偏差。起初,它作用很小,但随着时间的推移,这个值将逐渐增加(累积))并加入到运算中,随着时间的流逝它的作用将越来越明显。
我们不需要计算真正的积分。我们可不希望它的负无穷的起点或者是太长的时间间隔能够影响到物体现在的状态。
我们可以通过将最后几个周期的e(t)值相加然后与对应的时间间隔相乘(欧拉积分)或其它数值技术来估算短时间内的积分。在代码库中使用的是复合辛普森法则求积公式。
微分反馈
大部分PID控制器到了“PI”部分就停止了。比例的部分输入出现角度摇摆,积分部分能够对其产生一个不同方向的力来修正。然而,我们在输出时仍然有振荡响应。我们需要的是有一种方法去使物体缓慢朝着目标角度旋转。用比例和积分项来推动它。通过观察e(t)的导数,我们可以计算到它的值和知道应用力的方向不会改变。这是一个比例和积分部分的反力矩:
f(e(t))=Kp*e(t)+∫?∞nowKi*e(t)dt+Kd*de(t)dt
考虑到当e(t)出现振荡的时候。它表现得就像一个正弦函数。它的导数是一个余弦函数,其最大值出现在sin(e(t))= 0。也就是说,当e(t)摇摆时经过我们想要的位置时导数值是最大。相反,当处于振荡边缘,即将改变方向时,其速度变化方向由正转负(反之亦然),导数最小。所以微分项在物体到达我们想要的位置时造成的反扭矩最大,从而消除振荡,而在“摇摆”的边缘反扭矩则是最小值。
就像积分一样,微分项同样是可以被计算的数值。它是通过之前几个不同的e(t)值计算出来的(参见代码)。
注意:在真实的控制系统中使用微分项不是一个好主意。如果e(t)来回变化太快的话,使微分会因为往返变化出现误差,导致导数来回飙升。然而,在我们的案例中,除非数值出错,否则不会出现任何问题。
类和序列
因为我们要符合软件思想,无论我们使用何种算法来实现PID控制器,都想把它封装起来以便使用,给它一个清晰干净的界面,隐藏我们不需要的东西。转变成实体“拥有”的属性。
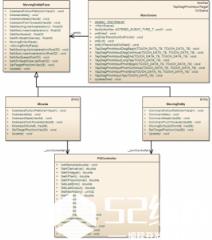
MovingEntityInterface代表一个“实体”。在这个示例中,它可以是一个导弹,只往前移动,或者一个可以在移动时转动的“物体”。虽然他们在内部有不同的方法“应用推力”,但他们都用几乎相同的方法来控制转向。这种折中的“寻找”行为更加符合实际。
接口本身是通用的,因此MainScene类可以有一个任何类型都能操作的实例。
PIDController类本身有这个接口:
#ifndef __Interpolator__PIDController__
#define __Interpolator__PIDController__
#include "CommonSTL.h"
#include "MathUtilities.h"
class PIDController
{
private:
double _dt;
uint32 _maxHistory;
double _kIntegral;
double _kProportional;
double _kDerivative;
double _kPlant;
vector _errors;
vector _outputs;
enum
{
MIN_SAMPLES = 3
};
double SingleStepPredictor(
double x0, double y0,
double x1, double y1,
double dt) const
{
assert(!MathUtilities::IsNearZero(x1-x0));
double m = (y1-y0)/(x1-x0);
double b = y1 - m*x1;
double result = m*(x1 + dt) + b;
return result;
}
void CalculateNextOutput()
{
if(_errors.size() < MIN_SAMPLES)
{ // We need a certain number of samples
// before we can do ANYTHING at all.
_outputs.push_back(0.0);
}
else
{ // Estimate each part.
size_t errorSize = _errors.size();
// Proportional
double prop = _kProportional * _errors[errorSize-1];
// Integral - Use Extended Simpson's Rule
double integral = 0;
for(uint32 idx = 1; idx < errorSize-1; idx+=2)
{
integral += 4*_errors[idx];
}
for(uint32 idx = 2; idx < errorSize-1; idx+=2)
{
integral += 2*_errors[idx];
}
integral += _errors[0];
integral += _errors[errorSize-1];
integral /= (3*_dt);
integral *= _kIntegral;
// Derivative
double deriv = _kDerivative * (_errors[errorSize-1]-_errors[errorSize-2]) / _dt;
// Total P+I+D
double result = _kPlant * (prop + integral + deriv);
_outputs.push_back(result);
}
}
public:
void ResetHistory()
{
_errors.clear();
_outputs.clear();
}
void ResetConstants()
{
_kIntegral = 0.0;
_kDerivative = 0.0;
_kProportional = 0.0;
_kPlant = 1.0;
}
PIDController() :
_dt(1.0/100),
_maxHistory(7)
{
ResetConstants();
ResetHistory();
}
void SetKIntegral(double kIntegral) { _kIntegral = kIntegral; }
double GetKIntegral() { return _kIntegral; }
void SetKProportional(double kProportional) { _kProportional = kProportional; }
double GetKProportional() { return _kProportional; }
void SetKDerivative(double kDerivative) { _kDerivative = kDerivative; }
double GetKDerivative() { return _kDerivative; }
void SetKPlant(double kPlant) { _kPlant = kPlant; }
double GetKPlant() { return _kPlant; }
void SetTimeStep(double dt) { _dt = dt; assert(_dt > 100*numeric_limits::epsilon());}
double GetTimeStep() { return _dt; }
void SetMaxHistory(uint32 maxHistory) { _maxHistory = maxHistory; assert(_maxHistory >= MIN_SAMPLES); }
uint32 GetMaxHistory() { return _maxHistory; }
void AddSample(double error)
{
_errors.push_back(error);
while(_errors.size() > _maxHistory)
{ // If we got too big, remove the history.
// NOTE: This is not terribly efficient. We
// could keep all this in a fixed size array
// and then do the math using the offset from
// the beginning and module math. But this
// gets complicated fast. KISS.
_errors.erase(_errors.begin());
}
CalculateNextOutput();
}
double GetlastError() { size_t es = _errors.size(); if(es == 0) return 0.0; return _errors[es-1]; }
double GetLastOutput() { size_t os = _outputs.size(); if(os == 0) return 0.0; return _outputs[os-1]; }
virtual ~PIDController()
{
}
};
这是一个用起来非常简单的类。可以根据需要调用SetKXXX函数,设置每个时间步的集成,并在每一帧调用AddSample(…)处理差值。
看着Missile类,拥有这样的一个实例,该变化步骤(在Update中)如下:
void ApplyTurnTorque()
{
Vec2 toTarget = GetTargetPos() - GetBody()->GetPosition();
float32 angleBodyRads = MathUtilities::AdjustAngle(GetBody()->GetAngle());
if(GetBody()->GetLinearVelocity().LengthSquared() > 0)
{ // Body is moving
Vec2 vel = GetBody()->GetLinearVelocity();
angleBodyRads = MathUtilities::AdjustAngle(atan2f(vel.y,vel.x));
}
float32 angleTargetRads = MathUtilities::AdjustAngle(atan2f(toTarget.y, toTarget.x));
float32 angleError = MathUtilities::AdjustAngle(angleBodyRads - angleTargetRads);
_turnController.AddSample(angleError);
// Negative Feedback
float32 angAcc = -_turnController.GetLastOutput();
// This is as much turn acceleration as this
// "motor" can generate.
if(angAcc > GetMaxAngularAcceleration())
angAcc = GetMaxAngularAcceleration();
if(angAcc < -GetMaxAngularAcceleration())
angAcc = -GetMaxAngularAcceleration();
float32 torque = angAcc * GetBody()->GetInertia();
GetBody()->ApplyTorque(torque);
}
细微差别
在导弹与对比物的跟踪路径有一个明显的不同(代码中的MovingEntity)。导弹容易越过给出的路线,尤其是当其最大转率降低。
MovingEntity总是更直接转向目的点,因为它是用一个“矢量反馈”自身位置与目标位置并调整速度。这比导弹更像传统的“寻找”行为。
很明显,我还遗漏了一些关于如何优化PID控制器常量的关键信息。在谷歌上有许多关于如何优化PID控制回路的文章,毕竟还要留待大家自己学习。
你或许也注意到_dt的默认值,时间间隔,设置为0.01秒。你可以调整该值匹配实际使用的时间间隔,你会遇到(舍入误差、系统带宽问题,等等)需要权衡的数值模拟。实际上,我在各种大小不同的物理实体上使用了相同的控制器及常量,而最终的行为都是足够真实的(到目前为止),因此我没有去细微的调整过参数。你的情况可能会和我不同。
这里的源代码,用Cocos2d-x/C++编写的,可以在github找到。PIDController类只依赖标准库,应该能移植到其他系统。






