今天小编给大家分享一下C++二叉树层序遍历实例分析的相关知识点,内容详细,逻辑清晰,相信大部分人都还太了解这方面的知识,所以分享这篇文章给大家参考一下,希望大家阅读完这篇文章后有所收获,下面我们一起来了解一下吧。
二叉树层序遍历
Example 1:
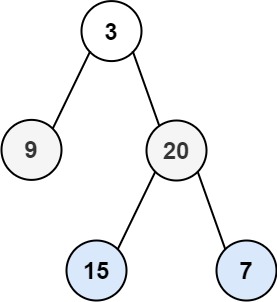
Input: root = [3,9,20,null,null,15,7]
Output: [[15,7],[9,20],[3]]
Example 2:
Input: root = [1]
Output: [[1]]
Example 3:
Input: root = []
Output: []
Constraints:
The number of nodes in the tree is in the range [0, 2000].
-1000 <= Node.val <= 1000
从底部层序遍历其实还是从顶部开始遍历,只不过最后存储的方式有所改变,可以参见博主之前的博文 Binary Tree Level Order Traversal, 参见代码如下:
解法一:
class Solution {public: vector<vector<int> > levelOrderBottom(TreeNode* root) { if (!root) return {}; vector<vector<int>> res; queue<TreeNode*> q{{root}}; while (!q.empty()) { vector<int> oneLevel; for (int i = q.size(); i > 0; --i) { TreeNode *t = q.front(); q.pop(); oneLevel.push_back(t->val); if (t->left) q.push(t->left); if (t->right) q.push(t->right); } res.insert(res.begin(), oneLevel); } return res; }};下面来看递归的解法,由于递归的特性,我们会一直深度优先去处理左子结点,那么势必会穿越不同的层,所以当要加入某个结点的时候,必须要知道当前的深度,所以使用一个变量 level 来标记当前的深度,初始化带入0,表示根结点所在的深度。由于需要返回的是一个二维数组 res,开始时由于不知道二叉树的深度,不知道有多少层,所以无法实现申请好二维数组的大小,只有在遍历的过程中不断的增加。那么什么时候该申请新的一层了呢,当 level 等于二维数组的大小的时候,为啥是等于呢,不是说要超过当前的深度么,这是因为 level 是从0开始的,就好比一个长度为n的数组A,你访问 A[n] 是会出错的,当 level 等于数组的长度时,就已经需要新申请一层了,新建一个空层,继续往里面加数字,参见代码如下:
解法二:
class Solution {public: vector<vector<int>> levelOrderBottom(TreeNode* root) { vector<vector<int>> res; levelorder(root, 0, res); return vector<vector<int>> (res.rbegin(), res.rend()); } void levelorder(TreeNode* node, int level, vector<vector<int>>& res) { if (!node) return; if (res.size() == level) res.push_back({}); res[level].push_back(node->val); if (node->left) levelorder(node->left, level + 1, res); if (node->right) levelorder(node->right, level + 1, res); }};以上就是“C++二叉树层序遍历实例分析”这篇文章的所有内容,感谢各位的阅读!相信大家阅读完这篇文章都有很大的收获,小编每天都会为大家更新不同的知识,如果还想学习更多的知识,请关注编程网行业资讯频道。





