这篇文章主要介绍Java如何实现的图的遍历,文中介绍的非常详细,具有一定的参考价值,感兴趣的小伙伴们一定要看完!
1.图的遍历
从图中某一顶点出发访问图中其余顶点,且每个顶点仅被访问一次
图的遍历有两种深度优先遍历DFS、广度优先遍历BFS
2.深度优先遍历
深度优先遍历以深度为优先进行遍历,简单来说就是每次走到底。类似于二叉树的前序遍历
思路:
以某一个顶点为起点进行深度优先遍历,并标记该顶点已访问
以该顶点为起点选取任意一条路径一直遍历到底,并标记访问过的顶点
第2步遍历到底后回退到上一个顶点,重复第2步
遍历所有顶点结束
根据遍历思路可知,这是一个递归的过程,其实DFS与回溯基本相同。
遍历:
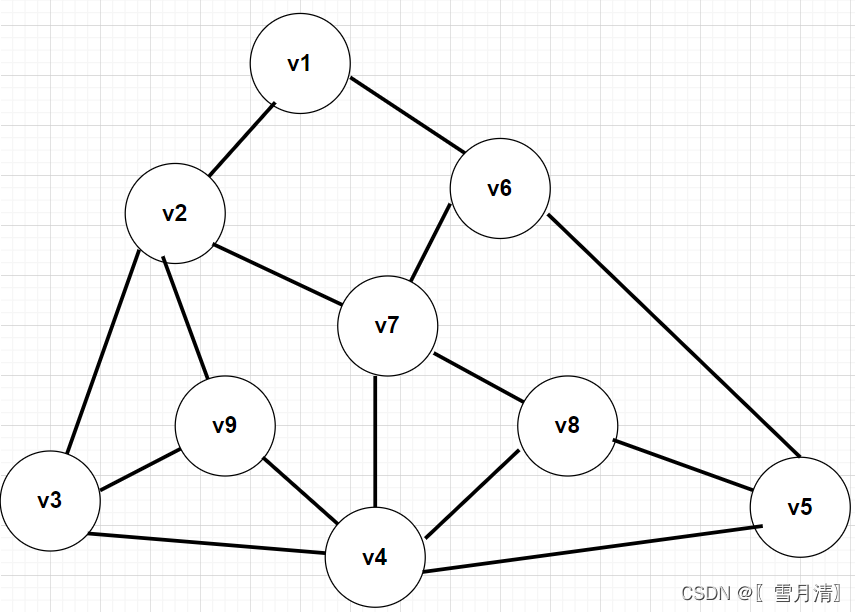
以此图为例进行深度优先遍历
static void dfs(int[][] graph,int idx,boolean[]visit) {int len = graph.length;//访问过 if(visit[idx]) return; //访问该顶点 System.out.println("V"+idx); //标志顶点 visit[idx] = true; for(int i = 1;i < len;i++) { //访问该顶点相连的所有边 if(graph[idx][i] == 1) { //递归进行dfs遍历 dfs(graph, i, visit); } }}遍历结果:
V1
V2
V3
V4
V5
V6
V7
V8
V9
创建图的代码:
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);//顶点数 以1开始int n = scanner.nextInt();int[][] graph = new int[n+1][n+1];//边数int m = scanner.nextInt();for(int i = 1;i <= m;i++) {int v1 = scanner.nextInt();int v2 = scanner.nextInt();graph[v1][v2] = 1;graph[v2][v1] = 1;}//标记数组 false表示未访问过 boolean[] visit = new boolean[n+1];dfs(graph, 1, visit);}3.利用DFS判断有向图是否存在环
思路:遍历某一个顶点时,如果除了上一个顶点之外,还存在其他相连顶点被访问过,则必然存在环
//默认无环 static boolean flag = false;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);//顶点数 以1开始int n = scanner.nextInt();int[][] graph = new int[n+1][n+1];//边数int m = scanner.nextInt();for(int i = 1;i <= m;i++) {int v1 = scanner.nextInt();int v2 = scanner.nextInt();graph[v1][v2] = 1;} //标记数组 true为访问过boolean[] visit = new boolean[n+1];dfs(graph, 1, visit,1);if(flag) System.out.println("有环");}static void dfs(int[][] graph,int idx,boolean[]visit,int parent) {int len = graph.length; System.out.println("V"+idx); //标记顶点 visit[idx] = true; for(int i = 1;i < len;i++) { //访问该顶点相连的所有边 if(graph[idx][i] == 1) { if( !visit[i] ) { dfs(graph, i, visit,idx); } else if(idx != i) { flag = true; } } } }注意:是有向图判断是否存在环,无向图判断是否存在环无意义,因为任意两个存在路径的顶点都可以是环
4.广度优先遍历
广度优先遍历是以广度(宽度)为优先进行遍历。类似于二叉树的层序遍历
思路:
以某一个顶点为起点进行广度优先遍历,并标记该顶点已访问
访问所有与该顶点相连且未被访问过的顶点,并标记访问过的顶点
以第2步访问所得顶点为起点重复1、2步骤
遍历所有顶点结束
通过队列来辅助遍历,队列出队顺序即是广度优先遍历结果
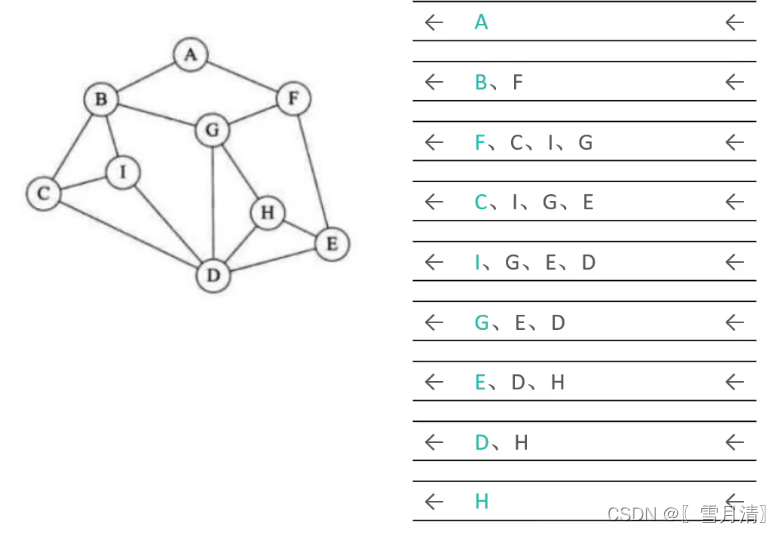
遍历
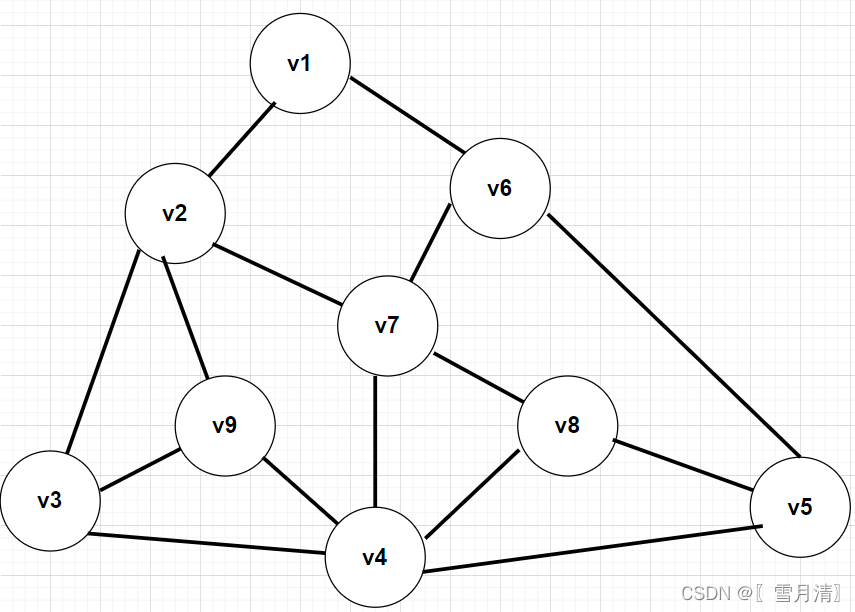
以此图为例,采用邻接矩阵的方式创建图,进行BFS遍历
static void bfs(int[][] graph) {int len = graph.length;//标记数组 false表示未访问过 boolean[] visit = new boolean[len];//辅助队列Queue<Integer> queue = new LinkedList<>();queue.offer(1);visit[1] = true;while(!queue.isEmpty()) {int num = queue.poll();System.out.println("V"+num);//遍历该顶点所有相连顶点for(int i = 1;i < len;i++) {//相连并且没有被访问过if(graph[num][i] == 1 && !visit[i]) {queue.offer(i);visit[i] = true;}}}}遍历结果:
V1
V2
V6
V3
V7
V9
V5
V4
V8
创建图的代码
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);//顶点数 以1开始int n = scanner.nextInt();int[][] graph = new int[n+1][n+1];//边数int m = scanner.nextInt();for(int i = 1;i <= m;i++) {int v1 = scanner.nextInt();int v2 = scanner.nextInt();graph[v1][v2] = 1;graph[v2][v1] = 1;}bfs(graph);}以上是“Java如何实现的图的遍历”这篇文章的所有内容,感谢各位的阅读!希望分享的内容对大家有帮助,更多相关知识,欢迎关注编程网行业资讯频道!










