这篇文章主要为大家展示了“python中逻辑回归限制的示例分析”,内容简而易懂,条理清晰,希望能够帮助大家解决疑惑,下面让小编带领大家一起研究并学习一下“python中逻辑回归限制的示例分析”这篇文章吧。
1.逻辑回归的限制
逻辑回归分类的时候,是把线性的函数输入进sigmoid函数进行转换,后进行分类,会在图上画出一条分类的直线,但像下图这种情况,无论怎么画,一条直线都不可能将其完全分开。
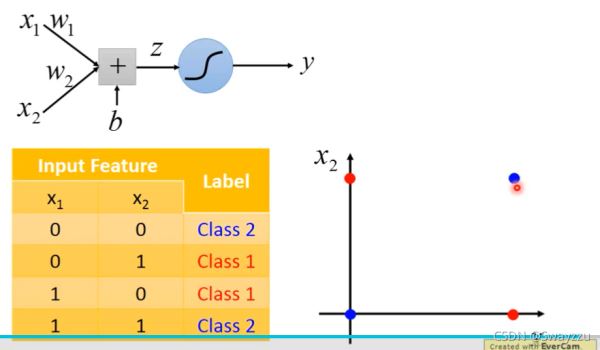
但假如我们可以对输入的特征进行一个转换,便有可能完美分类。比如:
创造一个新的特征x1:到(0,0)的距离,另一个x2:到(1,1)的距离。这样可以计算出四个点所对应的新特征,画到坐标系上如以下右图所示。这样转换之后,就可以将转换后的数据,输入给一个逻辑回归,将其完全分开。
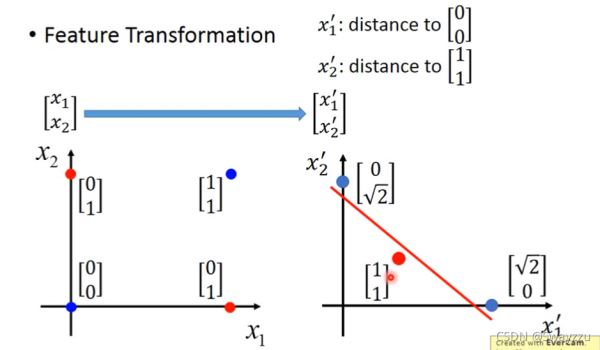
虽然我们不容易直接找到这样的一个转换标准,但我们可以通过逻辑回归去寻找标准,使用第一个逻辑回归,寻找第一个转换后的参数x1, 再使用第二个逻辑回归,寻找第二个转换后的参数x2,将这两个作为新的输入,给到第三个逻辑回归,即可完成分类。
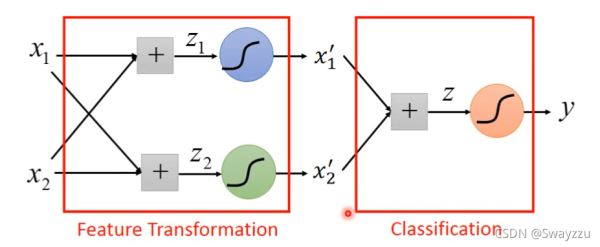
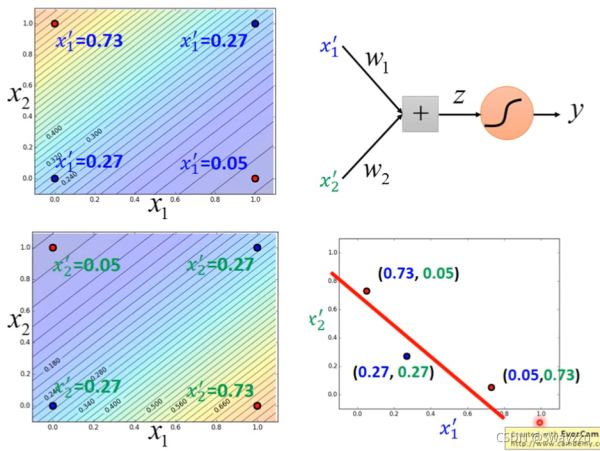
因此,我们可以通过参数的调整,使得输入的x1,x2归属于两类的概率(其实就是一个0-1中间的数字,我们暂且称为概率)如下图所示。那么左上角的点属于两类的概率就是(0.73,0.05),同理,其他的点也有属于两类的概率,将其放到坐标轴上,就完成了对特征的转换。将转换之后的结果作为输入,给到一个新的逻辑回归,就可以完成分类。
2.深度学习的引入
可以看出来,每一个逻辑回归单元,既可以作为接受者,接收输入数据,也可以作为发送者,将自己的输出结果作为其他的逻辑回归单元的输入数据。
多个逻辑回归单元交织在一起,就称为神经网络,每一个逻辑回归单元,就是一个神经元。这种学习方式,就叫做深度学习。
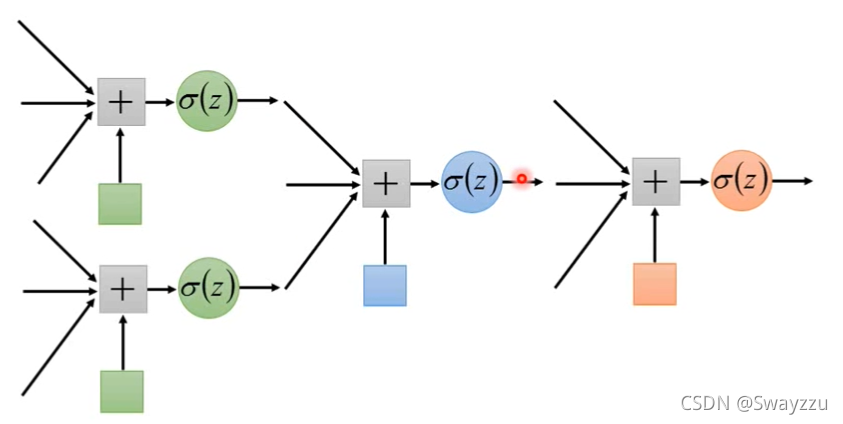
以下是一个例子:
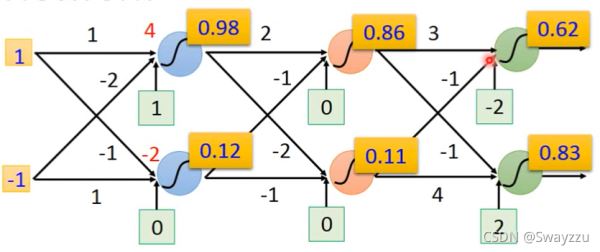
假设初始输入数据是1和-1,并且所有的权重我们都知道,比如两个数据到第一层两个神经元的权重分别是1,-1,-2, 1,然后通过sigmoid函数转换后,那么我们就可以计算出结果分别是0.98,0.12,同样的,假如我们知道后面所有的权重(参数),我们最终可以得到两个输出,0.62,0.83
当最开头的数据输入是0和0,通过同样的转换,可以得到输出0.51,0.85。可以看出,无论输入是什么样的,我们总能够通过一系列参数,进行一系列转换,将其输出成特征完全不一样的数据。
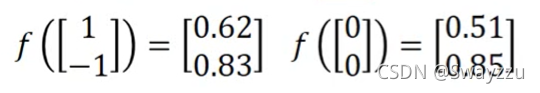
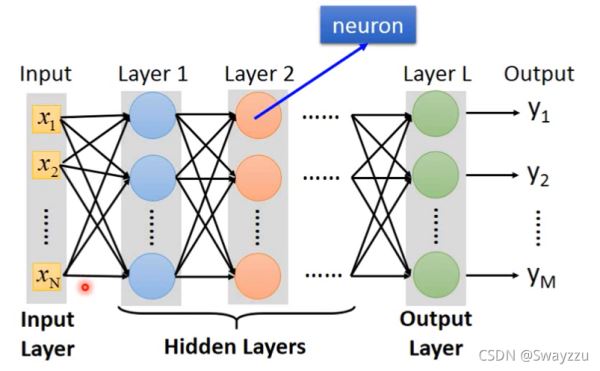
因此,整个网络可以看作是一个函数。更一般地,如下图所示,每一个圆圈都是一个神经元,最前面的输入叫做输入层,最后面没有接任何神经元的,叫做输出层,中间所有的叫做隐藏层。像下图这样每一个神经元都连接到下一层所有的神经元,叫做全连接神经网络。
3.深度学习的计算方式
对于深度学习,通常使用矩阵运算的方式进行计算。
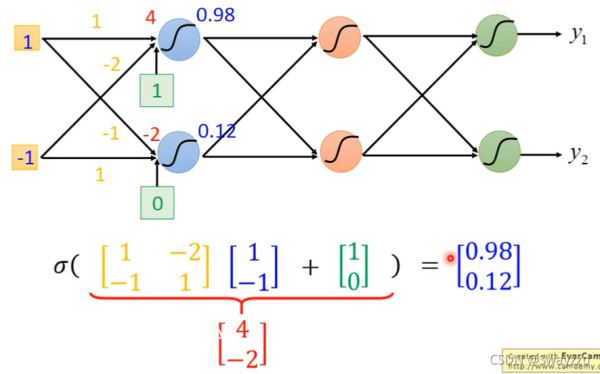
更一般地:
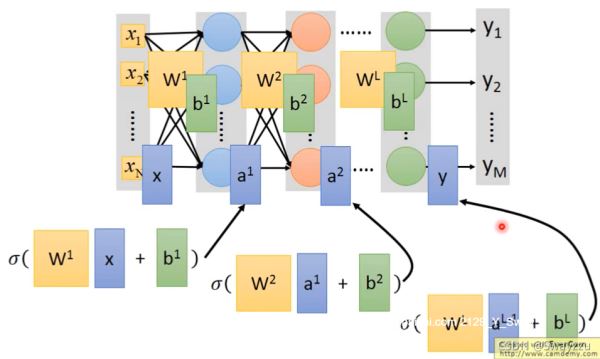
即上一层的参数*上一层给的输入值 + 偏置项,再对整体进行一个sigmoid函数转化,就可以输出一个本层的数据,供下层使用。对于所有的神经元均是一样的操作,一直到输出层。
4.神经网络的损失函数
对于一个样本来说,损失函数如下图所示:
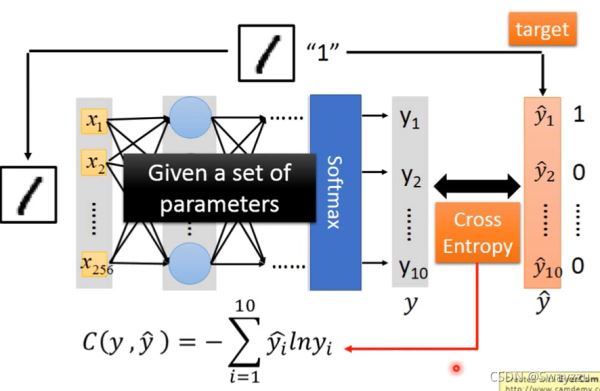
比如输入的是样本“1”,有256个像素点,也就是256个特征,将其输入神经网络,最终得到的输出是一个10维向量,每一个维度,都会有一个概率值,比如是“1”的概率为0.8, “2”的概率为0.1等等,而实际的标签是“1”,也就是只有y1hat是1,其他是0。将这两个向量求出交叉熵并求和,如上图的式子,得出的C就是这个样本的损失。
对于整体而言,把所有的样本损失算出来并求和即可。
以上是“python中逻辑回归限制的示例分析”这篇文章的所有内容,感谢各位的阅读!相信大家都有了一定的了解,希望分享的内容对大家有所帮助,如果还想学习更多知识,欢迎关注编程网行业资讯频道!




