卡方检验
1.卡方检验
卡方检验也属于假设检验的一种即可以分析一个变量的拟合程度,如拟合优度检验(二项分布、泊松分布和正态分布),即可以分析数据是不是正态分布,在做T检验的时候(前提条件就是数据要符合正态分布)。
还可以用来分析两个变量间的关系:是否相互独立,是否来自一个总体。
2.独立性卡方检验与一致性卡方检验
对于两个变量关系的分析方法与在拟合优度中的方法略有差别,这里适用了一种称为列联表的表格来进行分析。
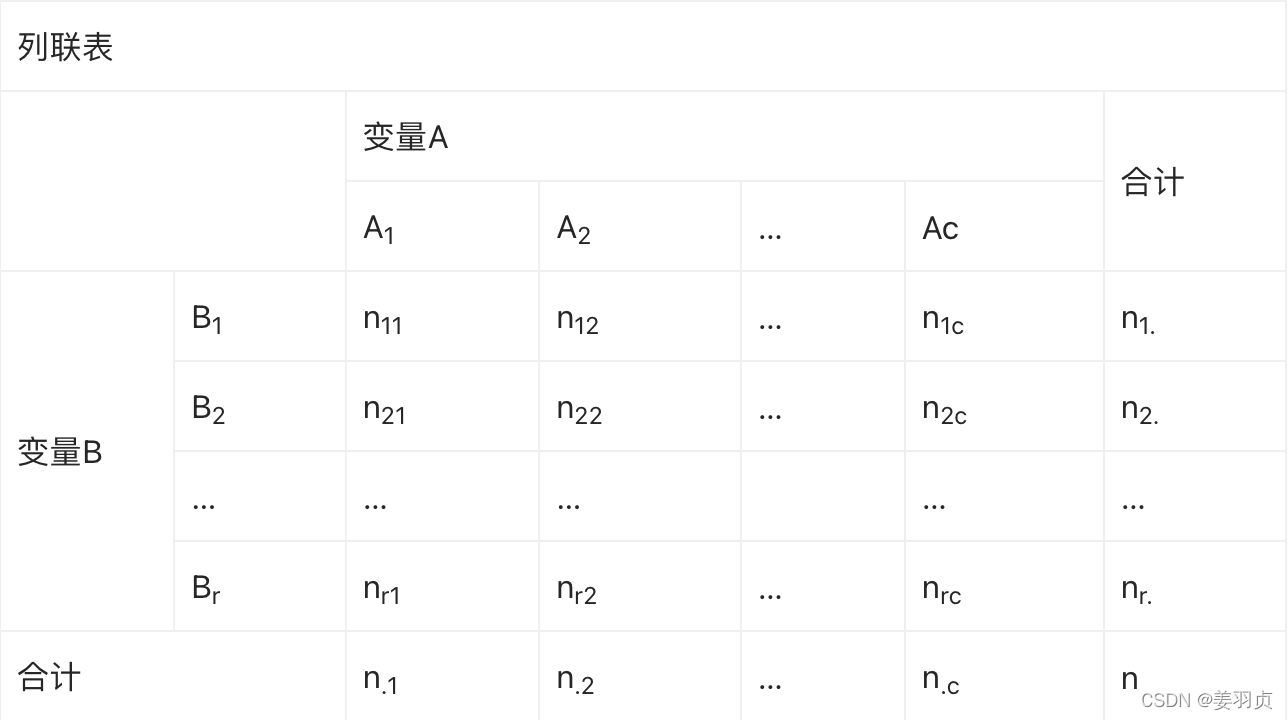
列联表
所谓列联表就是一个行列交叉的表格。将研究的两个变量,一个变量按类分行排列,另一个变量按类分列排列,行列交叉处是同属于两个变量不同类的数据。这样的表格称为列联表,这种类型的数据,也是做卡方检验所需要的数据
2.1 独立性卡方检验
下面举一个例子来说明下独立卡方检验如何运用的😎
比如说咖啡店,不同职业的人偏好不同口味的咖啡,老板想知道职业这个变量与不同口味咖啡是否独立。
数据如下图所示,在显著性为α=0.01下,检验职业与口味是否独立性
| IT | 行政 | 工程 | 合计 | |
|---|---|---|---|---|
| 美式咖啡 | 25 | 21 | 10 | 56 |
| 拿铁咖啡 | 82 | 88 | 30 | 200 |
| 卡布奇诺 | 223 | 16 | 5 | 244 |
| 合计 | 330 | 125 | 45 | 500 |
1.假设
H0 H_0 H0:职业与咖啡无关系(独立)
H1 H_1 H1:职业与咖啡有关系(不独立)
2.计算期望频数
本例中行与列的数相等,r=c=3是个3*3的列联表,所以需要计算9个期望频数值。根据上表数据,利用公式计算每一行列的期望频数。例如:
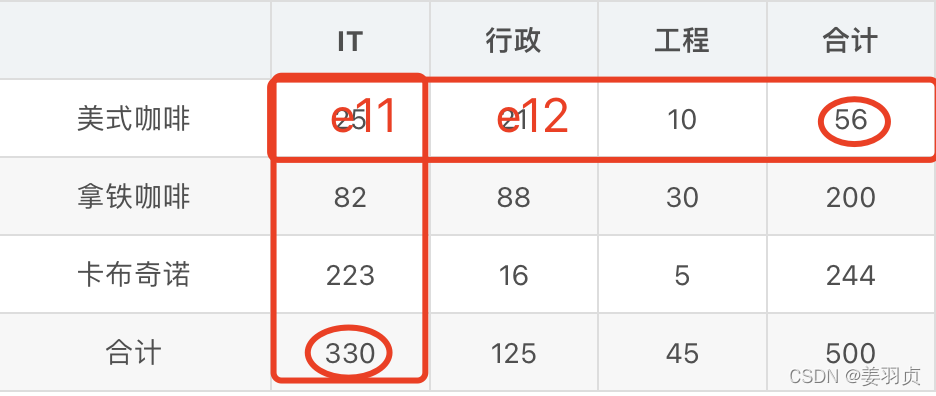
e11 = n 1... ∗ n . . . 1 n = 56 ∗ 330 500 = 36.96 e_{11}=\frac{n_{1...}*n_{...1}}{n}=\frac{56*330}{500}=36.96 e11=nn1...∗n...1=50056∗330=36.96
e12 = n 1... ∗ n . . . 2 n = 56 ∗ 125 500 = 14 e_{12}=\frac{n_{1...}*n_{...2}}{n}=\frac{56*125}{500}=14 e12=nn1...∗n...2=50056∗125=14
以此类推,可算出所有期望频数。
3.计算卡方值
e11 e_{11} e11对应的值减去 e11 的 平 方 e_{11}的平方 e11的平方
χ 2 = ( 25 − 36.96 ) 2 36.96 + ( 21 − 14 ) 2 14 + . . + ( 5 − 21.96 ) 2 21.96 = 138.21 χ2=\frac{(25-36.96)^2}{36.96}+\frac{(21-14)^2}{14}+..+\frac{(5-21.96)^2}{21.96}=138.21 χ2=36.96(25−36.96)2+14(21−14)2+..+21.96(5−21.96)2=138.21
已知α=0.01,查 χ 2 χ2 χ2分布表,得 χ 20.01 ( 4 ) = 12.277 χ2_{0.01}(4)=12.277 χ20.01(4)=12.277。因为 χ 2 = 138.21 > 12.277 = χ 20.01 ( 4 ) χ2=138.21>12.277=χ2_{0.01}(4) χ2=138.21>12.277=χ20.01(4),落在拒绝域。所以拒绝H0,接受H1,即职业和咖啡是关系的(不独立)
2.1.1 python独立性卡方检验
from scipy.stats import chi2_contingencyimport numpy as npimport pandas as pddata=[[25,21,10],[82,88,30],[223,16,5]]df=pd.DataFrame(data,index=['美式咖啡','拿铁咖啡','卡布奇诺'],columns=['IT','行政','工程'])kt=chi2_contingency(df)print('卡方值=%.4f, p值=%.4f, 自由度=%i expected_frep=%s'%kt)
p值小于0.01,则拒绝原假设,认为咖啡和职业不独立性。
2.2 一致性卡方检验
虽然表面看χ2的一致性检验方法与独立性检验方法一样,但两种检验方法在实质上还是有差别的。
二者差别:
- 两者检验的目的不同。独立性检验是对两个变量是否相关进行的检验,而一致性检验是对总体之间在某一变量分类中是否具相同分布的检验。
- 其次,两者抽样程序不同。独立性检验是从一个总体中抽出一个样本,然后按两个变量的类别进行分类;而一致性检验是从多个总体进行抽样,抽出多个样本,然后按不同样本进行分类
- 两种方法推断期望频数的理论不同。独立性检验是基于独立事件的假设推出期望频数,而一致性检验是基于不同总体具有相同的概率的假设推出期望频数。
举例说明:
研究职业与咖啡口味的关系时,如果关心的是职业与咖啡是否有关系,则应进行独立性检验。随机抽取一个人群样本后,将职业和咖啡口味分为不同的组,形成列联表进行检验。
研究是不同职业组对不同咖啡口味的要求是否一致,则应进行一致性检验。在不同职业组中进行抽样。把每一个职业组作为一个类别,检验在不同咖啡口味上的分布是否一致。
还是那上面那个数据举例,计算过程是一样的,只是在假设上有点差异。
1.假设
H0 H_0 H0:不同职业的咖啡口味一致
H1 H_1 H1:不同职业的咖啡口味不一致
3.正态分布卡方检验
其实还有柏松分布卡方检验和多项分布卡方检验,后续更进。

正态分布卡方检验属于非参数方法,
非参数法:通过样本信息来检验未知总体是否为某一种分布(正态分布,均匀分布或任意分布)
非参数方法是通过对比样本的频数与期望频数(目标分布的频数)的差距来判断抽取样本的总体分布是否为目标分布
下面举一个例子来说明下独立卡方检验如何运用的😎
有这样一组数据40件商品的质量:
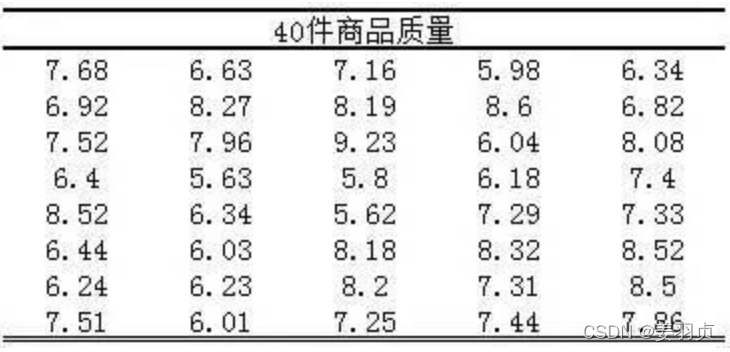
现在要看下这组数据是否服从正态分布。
1.假设
H0 H_0 H0:数据质量服从正态分布
H1 H_1 H1:数据质量不服从正态分布
α=0.05
2.计算正态分布区间界限
我们假设服从正态分布,从这组数据中求出数据的均值和标准差,用这二个数据,结合标准正态分布表,生成一个标准正态分布的数据出来:
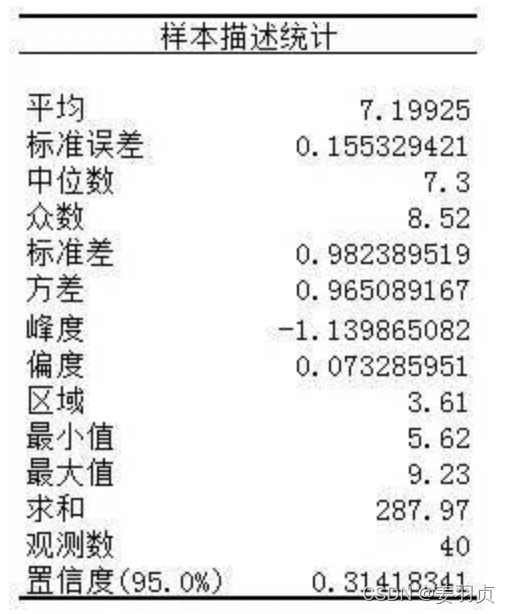
 为标准正态分布划分出几个区间(那为标准的正态分布划分8个区间,每个区间5个数据,在上图只有8个区间)
为标准正态分布划分出几个区间(那为标准的正态分布划分8个区间,每个区间5个数据,在上图只有8个区间)
8个区间对应的临界值所对应的X值(区间界限),如下图
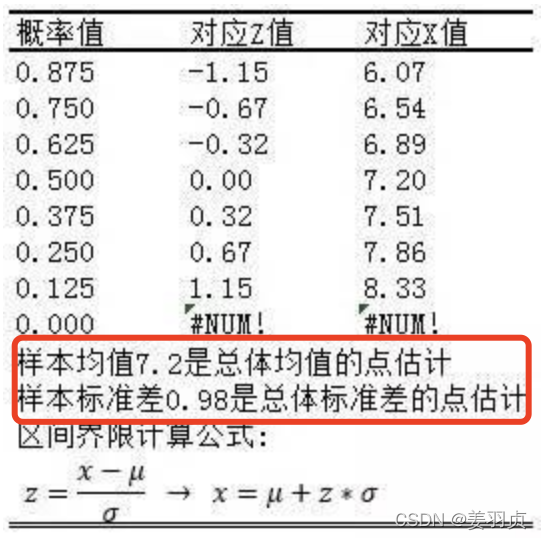
3.计算卡方值
根据计算的区间界限,将样本数据的每一个数据都分配到对应的区间中,然后统计实际频数。最后由实际频数与期望频数的差值计算卡方统计量,计算过程如下表:
χ 2 = ( O i − E i ) 2 E i χ2=\frac{(O_i-E_i)^2}{E_i} χ2=Ei(Oi−Ei)2
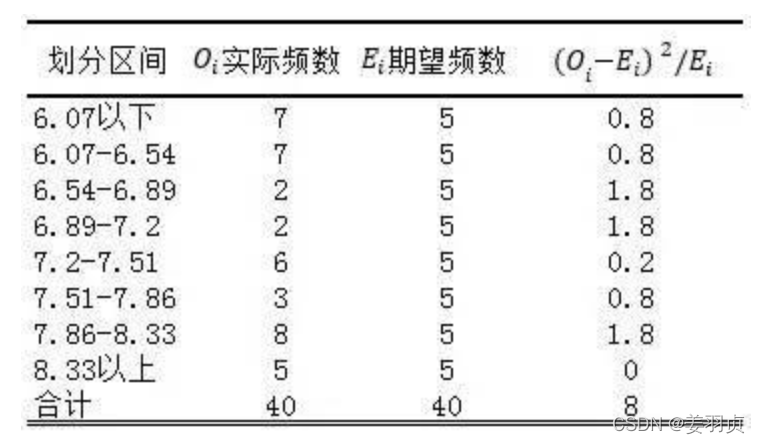
自由度:k-r-1,本例中,划分了8个区间k=8,估计了2个总体参数和σ,所以r=2,自由度为8-2-1=5
查卡方分布表(双侧显著水平0.5/2=0.025,自由度为5)得卡方值为11.07。因为计算卡方统计量为8<11.07,落在接受域,所以接受原假设,拒绝备择假设,即质量的数据可以认为是正态分布。
总结一下
就是根据实际的数据,算出的均值与标准差,去拟合一个标准的正态分布数据,因为标准的正态分布,每个区间的数据是均匀的,
然后在将实际的数据落在的标准正态分布的区间。计算不同区间的数据个数与标准正态的数据个数,代人求卡方值。
3.1 python正态分布卡方检验
import scipy from statsdf=[7.68,6.63,7.16,5.98,6.34, 6.92,8.27,8.19,8.6,6.82, 7.52,7.96,9.23,6.04,8.08, 6.4,5.63,5.8,6.18,7.4, 8.52,6.34,5.62,7.29,7.33, 6.44,6.03,8.18,8.32,8.52, 6.24,6.23,8.2,7.31,8.5, 7.51,6.01,7.25,7.44,7.86]ks_test = stats.kstest(df,'norm')shapiron_test = stats.shapiro(df)print('ks_test: ',ks_test)print('shapiro_test: ',shapiron_test)
这二种方法都可以ks_test、shapiron_test,看p值
p值>0.05,接受原假设服从正态分布
来源地址:https://blog.csdn.net/weixin_42010722/article/details/124296654







